Description
fx products
Managing Currency Risks
with Options
John W. Labuszewski
m a n ag i n g d i r ector
R e s e a rc h a n d p ro d u ct d e v e lo p m e n t
jlab@cmegroup.com
. cmegroup.com/fx
This represents an overview of our currency
options and how they can be deployed in a risk
management program.
CME Group’s Exchanges have offered options exercisable for
currency futures dating back to 1982. Like the Exchange’s family
of currency futures products, these options may be used as an
effective and efficient tool to manage currency or FX risks in an
uncertain world.
In particular, options provide a tremendous amount of flexibility
closely to tailor one’s risk management program to one’s market
forecast. This flexibility is enhanced to the extent that we offer
these options on state-of-the-art CME Globex electronic trading
platforms coupled with the financial sureties afforded by its
centralized clearing system.
This document is intended to provide an overview of the mechanics
of our options on currency futures. Further, we offer a review of
various strategies and applications that may be deployed in the
context of a corporate currency management program.
Currency Option Fundamentals
Note that upon exercise, rather than delivering actual currency,
our options contemplate the establishment of a currency futures
position.
These contracts are accessible through the CME Globex electronic trading platform. Exchange traded options are similar to exchange traded futures with respect to their relatively high degree of standardization. And like currency futures, trading volumes in options on currency futures have been growing very quickly in recent years. What is an Option? – Options provide a very flexible structure that may be tailor made to meet the risk management or speculative needs of the moment.
Options may generally be categorized as two types: calls and puts … with two very different risk/reward scenarios. 1 There are two types of options: call options and put options. Call options convey the right, but not the obligation, to buy a specified quantity currency at a particular strike or exercise price on or before an expiration date. One may either buy a call option, paying a negotiated price or premium to the seller, writer or grantor of the call; or, sell, write or grant a call, thereby receiving that premium. Put options convey the right, but not the obligation, to sell a specified quantity currency at a particular strike or exercise price on or before an expiration date.
Again, one may buy or sell a put option, either paying or receiving a negotiated premium or price. Buying a call is a bullish transaction; selling a call is bearish. Options may be configured as European- or American-style options. A European-style option may only be exercised on its expiration date while an American-style option may be exercised at any time up to and including the expiration date. We offer options on FX futures configured in both American- and European-styles. The purchase of a call option is an essentially bullish transaction with limited downside risk. If the market should advance above the strike price, the call is considered “in-the-money” and one may exercise the call by purchasing currency at the exercise price even when the exchange rate exceeds the exercise price.
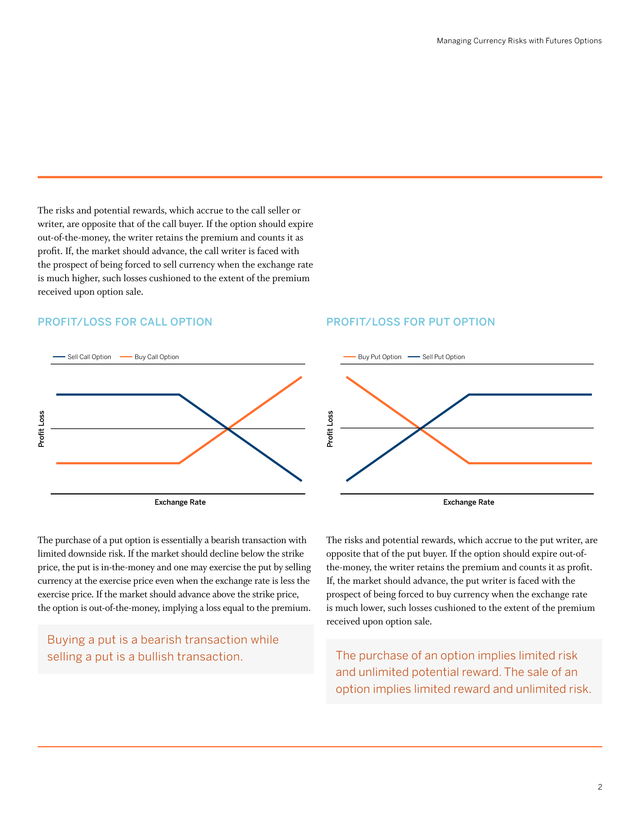
This implies a profit that is diminished only by the premium paid up front to secure the option. If the market should decline below the strike price, the option is considered “out-of-the-money” and may expire, leaving the buyer with a loss limited to the premium. . Managing Currency Risks with Futures Options The risks and potential rewards, which accrue to the call seller or writer, are opposite that of the call buyer. If the option should expire out-of-the-money, the writer retains the premium and counts it as profit. If, the market should advance, the call writer is faced with the prospect of being forced to sell currency when the exchange rate is much higher, such losses cushioned to the extent of the premium received upon option sale. Profit/loss for call option Buy Put Option Sell Put Option Proï¬t Loss Buy Call Option Proï¬t Loss Sell Call Option Profit/loss for Put option Exchange Rate The purchase of a put option is essentially a bearish transaction with limited downside risk. If the market should decline below the strike price, the put is in-the-money and one may exercise the put by selling currency at the exercise price even when the exchange rate is less the exercise price.
If the market should advance above the strike price, the option is out-of-the-money, implying a loss equal to the premium. Buying a put is a bearish transaction while selling a put is a bullish transaction. Exchange Rate The risks and potential rewards, which accrue to the put writer, are opposite that of the put buyer. If the option should expire out-ofthe-money, the writer retains the premium and counts it as profit. If, the market should advance, the put writer is faced with the prospect of being forced to buy currency when the exchange rate is much lower, such losses cushioned to the extent of the premium received upon option sale. The purchase of an option implies limited risk and unlimited potential reward. The sale of an option implies limited reward and unlimited risk. 2 .
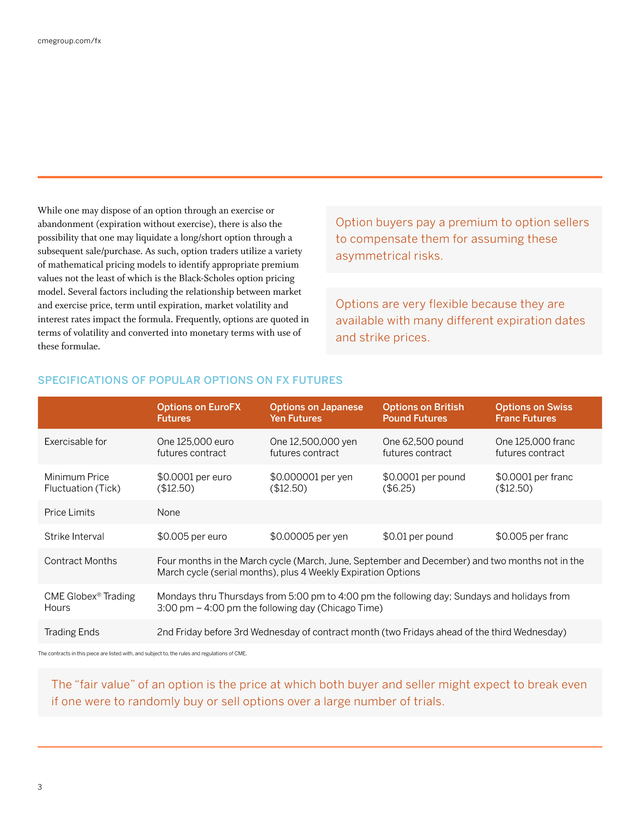
cmegroup.com/fx While one may dispose of an option through an exercise or abandonment (expiration without exercise), there is also the possibility that one may liquidate a long/short option through a subsequent sale/purchase. As such, option traders utilize a variety of mathematical pricing models to identify appropriate premium values not the least of which is the Black-Scholes option pricing model. Several factors including the relationship between market and exercise price, term until expiration, market volatility and interest rates impact the formula. Frequently, options are quoted in terms of volatility and converted into monetary terms with use of these formulae. Option buyers pay a premium to option sellers to compensate them for assuming these asymmetrical risks. Options are very flexible because they are available with many different expiration dates and strike prices. Specifications of Popular Options on FX Futures Options on EuroFX Futures Options on Japanese Yen Futures Options on British Pound Futures Options on Swiss Franc Futures Exercisable for One 125,000 euro futures contract One 12,500,000 yen futures contract One 62,500 pound futures contract One 125,000 franc futures contract Minimum Price Fluctuation (Tick) $0.0001 per euro ($12.50) $0.000001 per yen ($12.50) $0.0001 per pound ($6.25) $0.0001 per franc ($12.50) Price Limits None Strike Interval $0.005 per euro $0.00005 per yen $0.01 per pound $0.005 per franc Contract Months Four months in the March cycle (March, June, September and December) and two months not in the March cycle (serial months), plus 4 Weekly Expiration Options CME Globex® Trading Hours Mondays thru Thursdays from 5:00 pm to 4:00 pm the following day; Sundays and holidays from 3:00 pm – 4:00 pm the following day (Chicago Time) Trading Ends 2nd Friday before 3rd Wednesday of contract month (two Fridays ahead of the third Wednesday) The contracts in this piece are listed with, and subject to, the rules and regulations of CME. The “fair value” of an option is the price at which both buyer and seller might expect to break even if one were to randomly buy or sell options over a large number of trials. 3 .
Managing Currency Risks with Futures Options Because of the variety with which options are offered including puts and calls with varying exercise prices and expiration dates, one may create an almost infinite variety of strategies which may be tailored to suit one’s unique needs. Further, one deploys a combination of options to achieve particular risk management requirements. The intrinsic value of an option is equal to its in-the-money amount. If the option is out of the money, it has no intrinsic or in-the-money value. The intrinsic value is equivalent, and may be explained, by reference to the option’s “terminal value.” The terminal value of an option is the price the option would command just as it is about to expire. Option Pricing – Option pricing is at once one of the most complicated, but perhaps the most significant, topics that a prospective option trader can consider. The importance of being able to identify the “fair value” of an option is evident when you consider the meaning of the term “fair value” in the context of this subject. When an option is about to expire, an option holder has two alternatives available to him.
On one hand, the holder may elect to exercise the option or, on the other hand, may allow it to expire unexercised. Because the holder cannot continue to hold the option in the hopes that the premium will appreciate and the option may be sold for a profit, the option’s value is limited to whatever profit it may generate upon exercise. But how can a trader recognize over or under-priced options? What variables impact upon this assessment? There are a number of mathematical models, which may be used to calculate these figures, notably including models introduced by Black Scholes, Cox Ross Rubinstein and Whaley amongst others. The purpose of this section, however, is not to describe these models but to introduce some of the fundamental variables which impact upon an option premium and their effect.
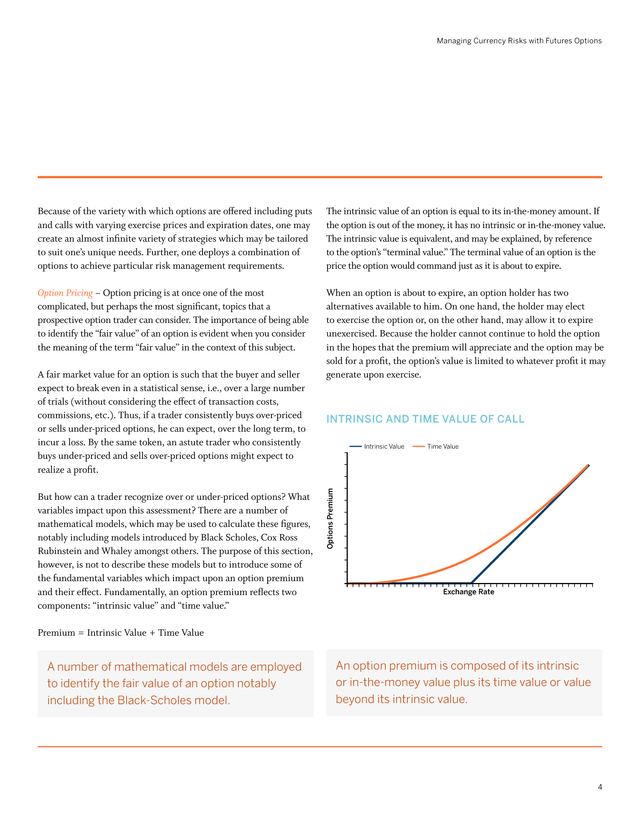
Fundamentally, an option premium reflects two components: “intrinsic value” and “time value.” Intrinsic and time value of call Intrinsic Value Time Value Options Premium A fair market value for an option is such that the buyer and seller expect to break even in a statistical sense, i.e., over a large number of trials (without considering the effect of transaction costs, commissions, etc.). Thus, if a trader consistently buys over-priced or sells under-priced options, he can expect, over the long term, to incur a loss. By the same token, an astute trader who consistently buys under-priced and sells over-priced options might expect to realize a profit. Exchange Rate Premium = Intrinsic Value + Time Value A number of mathematical models are employed to identify the fair value of an option notably including the Black-Scholes model. An option premium is composed of its intrinsic or in-the-money value plus its time value or value beyond its intrinsic value. 4 .
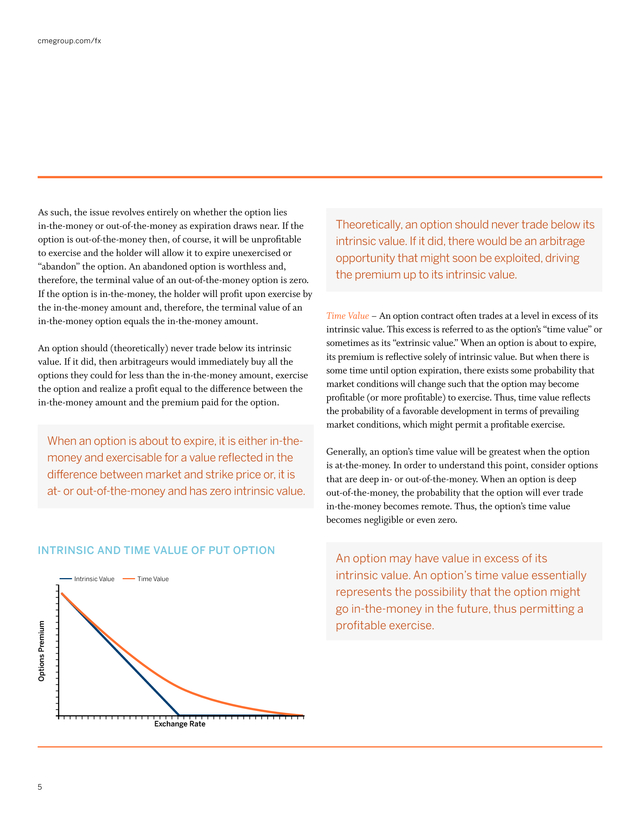
cmegroup.com/fx As such, the issue revolves entirely on whether the option lies in-the-money or out-of-the-money as expiration draws near. If the option is out-of-the-money then, of course, it will be unprofitable to exercise and the holder will allow it to expire unexercised or “abandon” the option. An abandoned option is worthless and, therefore, the terminal value of an out-of-the-money option is zero. If the option is in-the-money, the holder will profit upon exercise by the in-the-money amount and, therefore, the terminal value of an in-the-money option equals the in-the-money amount. An option should (theoretically) never trade below its intrinsic value. If it did, then arbitrageurs would immediately buy all the options they could for less than the in-the-money amount, exercise the option and realize a profit equal to the difference between the in-the-money amount and the premium paid for the option. When an option is about to expire, it is either in-themoney and exercisable for a value reflected in the difference between market and strike price or, it is at- or out-of-the-money and has zero intrinsic value. Intrinsic and time value of put option Time Value Options Premium Intrinsic Value Exchange Rate 5 Theoretically, an option should never trade below its intrinsic value.
If it did, there would be an arbitrage opportunity that might soon be exploited, driving the premium up to its intrinsic value. Time Value – An option contract often trades at a level in excess of its intrinsic value. This excess is referred to as the option’s “time value” or sometimes as its “extrinsic value.” When an option is about to expire, its premium is reflective solely of intrinsic value. But when there is some time until option expiration, there exists some probability that market conditions will change such that the option may become profitable (or more profitable) to exercise.
Thus, time value reflects the probability of a favorable development in terms of prevailing market conditions, which might permit a profitable exercise. Generally, an option’s time value will be greatest when the option is at-the-money. In order to understand this point, consider options that are deep in- or out-of-the-money. When an option is deep out-of-the-money, the probability that the option will ever trade in-the-money becomes remote.
Thus, the option’s time value becomes negligible or even zero. An option may have value in excess of its intrinsic value. An option’s time value essentially represents the possibility that the option might go in-the-money in the future, thus permitting a profitable exercise. . Managing Currency Risks with Futures Options When an option trades deep in-the-money, the leverage associated with the option declines. Leverage is the ability to control a large amount of resources with a relatively modest investment. Consider the extraordinary case where a call option has a strike price of zero. Under these circumstances, the option’s intrinsic value equals the outright purchase price of the instrument. There is no leverage associated with this option and, therefore, the option trader might as well simply buy the underlying instrument outright.
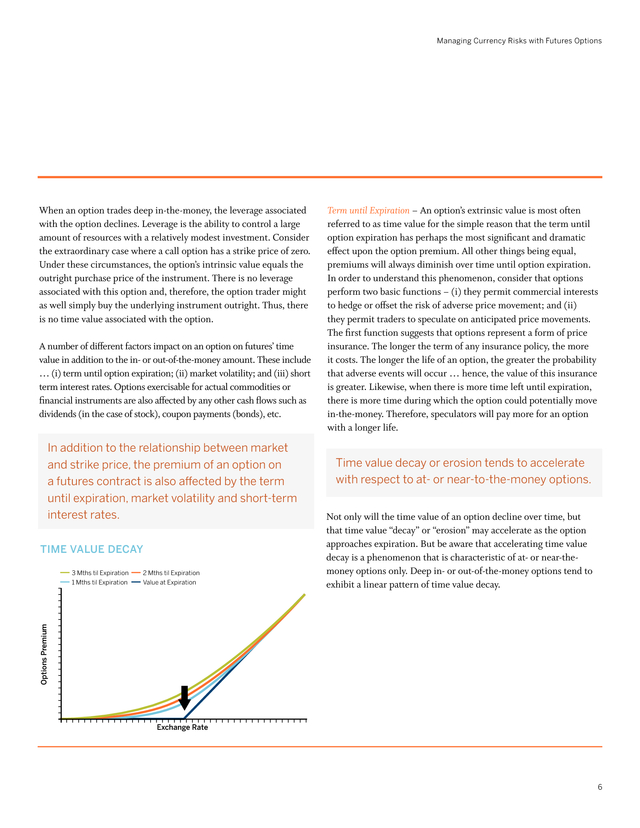
Thus, there is no time value associated with the option. A number of different factors impact on an option on futures’ time value in addition to the in- or out-of-the-money amount. These include … (i) term until option expiration; (ii) market volatility; and (iii) short term interest rates. Options exercisable for actual commodities or financial instruments are also affected by any other cash flows such as dividends (in the case of stock), coupon payments (bonds), etc. In addition to the relationship between market and strike price, the premium of an option on a futures contract is also affected by the term until expiration, market volatility and short-term interest rates. Time Value Decay 2 Mths til Expiration Value at Expiration Time value decay or erosion tends to accelerate with respect to at- or near-to-the-money options. Not only will the time value of an option decline over time, but that time value “decay” or “erosion” may accelerate as the option approaches expiration.
But be aware that accelerating time value decay is a phenomenon that is characteristic of at- or near-themoney options only. Deep in- or out-of-the-money options tend to exhibit a linear pattern of time value decay. Options Premium 3 Mths til Expiration 1 Mths til Expiration Term until Expiration – An option’s extrinsic value is most often referred to as time value for the simple reason that the term until option expiration has perhaps the most significant and dramatic effect upon the option premium. All other things being equal, premiums will always diminish over time until option expiration. In order to understand this phenomenon, consider that options perform two basic functions – (i) they permit commercial interests to hedge or offset the risk of adverse price movement; and (ii) they permit traders to speculate on anticipated price movements. The first function suggests that options represent a form of price insurance.
The longer the term of any insurance policy, the more it costs. The longer the life of an option, the greater the probability that adverse events will occur … hence, the value of this insurance is greater. Likewise, when there is more time left until expiration, there is more time during which the option could potentially move in-the-money.
Therefore, speculators will pay more for an option with a longer life. Exchange Rate 6 . cmegroup.com/fx Volatility impacts an option’s time value to the extent that it measures the extent to which the underlying market price may fluctuate, possibly driving the option into-the-money. Volatility – Option holders can profit when options trend into the money. If currency values are expected to move upwards by 10%, option traders would become inclined to buy call options. But if currency values were expected to move upwards by 20% over the same time period, traders would become even more anxious to buy calls, bidding the premium up in the process. It is not always easy to predict the direction in which prices will move, but it may nonetheless be possible to measure volatility. Market volatility is often thought of as price movement in either direction, up or down. In this sense, it is the magnitude, not the direction, of the movement that counts. Standard deviation is a statistic that is often employed to measure volatility.
For example, you may see a volatility assessed at 10%, 15%, 20%, etc. The use of this statistic implies that commodity price movements may be modeled by the “normal price distribution.” The normal distribution is represented by the familiar bell shaped curve. To interpret a volatility of 19%, for example, you can say with approximately 68% certainty that the price of the underlying instrument will be within plus or minus 19% of where it is now at the conclusion of a year. Or, with a probability of 95%, that the price of the underlying instrument will be within plus or minus 38% (2 x 19%) of where the price lies now at the conclusion of a year.
A good rule of thumb is that the greater the price volatility, the more the option will be worth. 7 Volatility is typically measured by the annualized standard deviation of percentage movements in the underlying market price. Short Term Rates – Whenever someone invests in any venture some positive return typically is expected. Accordingly, when an option exercisable for a futures contract is purchased there is an investment equal to the premium. To the extent that the option is paid for up front and in cash, a return is expected on the investment.
This implies that premiums must be discounted to reflect the lost opportunity represented by an investment in options. When the opportunity cost rises, as reflected in the rate at which funds may alternately be invested on a short term basis, the price of an option is discounted accordingly. When the opportunity cost decreases, the premium appreciates. When you buy an option, you pay cash. Shortterm interest rates play a role in determining the option premium because they reflect the opportunity costs associated with committing that cash to options. These remarks must be qualified by the following considerations: First, the effect described is applicable only to options on futures and not to options exercisable for actual instruments.
In fact, rising short term rates will tend to increase call premiums and decrease put premiums for options exercisable for actual instruments. Secondly, these remarks apply holding all other considerations equal. But of course, we know that all else is never held equal. For example, if short term rates are rising or falling, this suggests that bond futures prices will be affected.
Of course, this consideration will also have an impact, often much greater in magnitude, than the impact of fluctuating short term rates. . Managing Currency Risks with Futures Options Delta – When the price of the underlying instrument rises, call premiums rise and put premiums fall. But by how much? The change in the premium relative to the change in the underlying commodity price is measured by a common option statistic known as “delta.” Delta is generally expressed as a number from zero to 1.0. Deep in-the-money deltas will approach 1.0. Deep out-of-the-money deltas will approach zero. Finally at- or near-the-money deltas will run at about 0.50. Delta Deep In-the-money ⇒ At-the-Money ⇒ Deep Out-of-the-Money ⇒ 1.00 0.50 0.00 It is easy to understand why a deep in- or out-of-the-money option may have a delta equal to 1.0 or zero, respectively.
A deep in-themoney premium is reflective solely of intrinsic or in-the-money value. If the option moves slightly more or less in-the-money, its time value may be unaffected. Its intrinsic value, however, reflects the relationship between the market price and the fixed strike price. Hence, a delta of 1.0. Movements in the price of the instrument for which an option may be exercised are probably the most significant factor impacting an option premium.
Delta measures the expected change in the premium given a change in the underlying market price. At the other extreme, a deep out-of-the-money option has no value and is completely unaffected by slightly fluctuating market prices. Hence, a delta of zero. A call delta of 0.50 suggests that if the value of the underlying instrument advances by $1, the premium will advance by 50 cents. A put delta of 0.50 suggests that if the value of the underlying instrument advances by $1, the premium will fall by 50 cents. Delta is measured on a scale from 0 to 1. Deep inthe-money options will have deltas that approach 1 while deep out-of-the-money options will have deltas that approach zero. At-the-money options will tend to have deltas near 0.5. Delta is a dynamic concept.
It will change as the market price moves upwards or downwards. Hence, if an at-the-money call starts trending into the money, its delta will start to climb. Or, if the market starts falling, the call delta will likewise fall. “Greek” Statistics – In addition to movement in the underlying market price (as measured by delta), other factors impact significantly upon the option premium, notably including time until expiration and marketplace volatility.
A number of exotic “Greek” statistics including delta, gamma, vega and theta are often referenced to measure the impact of these factors upon the option premium. Underlying price movement stands out as perhaps the most obvious factor impacting option premiums and we have already discussed delta as the measure of such impact. Let’s consider other statistics including gamma, vega and theta. 8 .
cmegroup.com/fx Option premiums respond to fluctuations with respect to price, time and volatility. A number of statistics including delta, gamma, theta and vega are referenced to measure the responsiveness of option premiums to these factors. Gamma may be thought of as the “delta of the delta.” Gamma measures the expected change in the delta given a change in the underlying market price. Gamma is said to measure a phenomenon known as “convexity.” Convexity refers to the shape of the curve, which depicts the total value of an option premium over a range in possible underlying market values. The curvature of that line is said to be convex, hence the term convexity. “Greek” OPtion Statistics Delta Measures the expected change in the option premium given a change in the PRICE of the instrument underlying the option Gamma Measures the change in the DELTA given a change in the PRICE of the instrument underlying the option, i.e., the “delta of the delta” measuring a phenomenon known as “Convexity” Vega Measures the expected change in the option premium given a change in VOLATILITY of the instrument underlying the option Theta Measures the expected change in the option premium given the forward movement of TIME Gamma is the “delta of the delta,” measuring the prospective change in the delta given a change in the underlying market price.
Gamma is said to measure “convexity.” Convexity is a concept, which promises to benefit traders who purchase options to the detriment of those who sell or write options. Consider that as the market rallies, the premium advances at an ever-increasing rate as the delta itself advances. Thus, the holder of a call is making money at an increasing or accelerating rate.
But if the market should fall, the call holder is losing money, but at a decelerating rate. 9 On August 18, 2008, for example, the delta for a December 2008 1.4600 call (essentially at-the-money with December futures trading at 1.4605) was 0.5104. It had a gamma of 0.0478 suggesting that if the underlying futures price were to move upwards (downwards) by 1 cent, the value of delta would move upwards (downwards) by about 0.0478. This may be validated by noting that the call struck at 1.4500 has a delta of 0.5579 or 0.0475 higher than 0.5104.
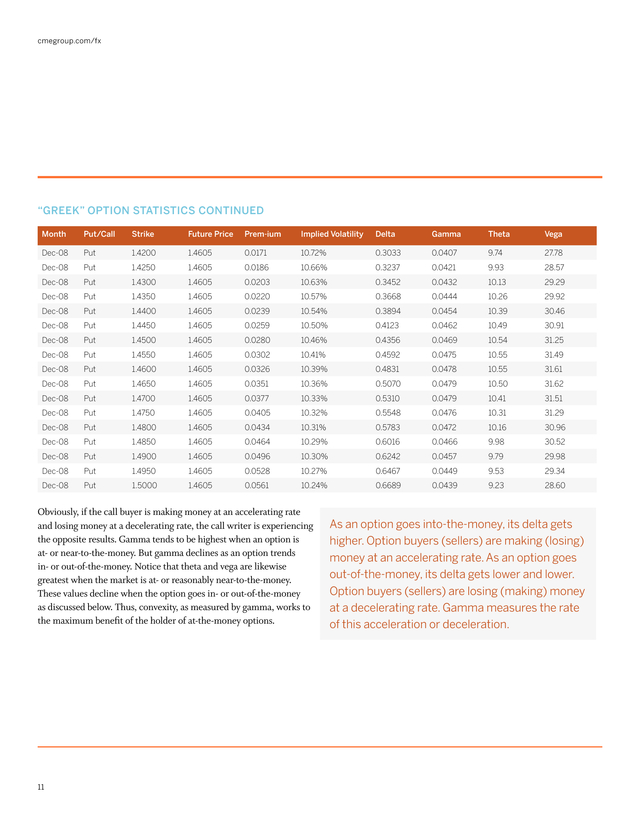
Or, that the call struck at 1.4700 has a delta of 0.4625 or 0.0479 lower than 0.5104. It is important to note that the gammas in our illustration are based upon a 1 cent or $0.01 movement in the EUR/USD exchange rate. The convexity property of options benefits option buyers to the detriment of option sellers. . Managing Currency Risks with Futures Options “Greek” OPtion Statistics Month Put/Call Strike Future Price Prem-ium Implied Volatility Delta Gamma Theta Vega Sep-08 Call 1.4400 1.4675 0.0320 11.07% 0.7819 0.0810 20.61 9.57 Sep-08 Call 1.4450 1.4675 0.0281 10.95% 0.7407 0.0910 22.41 10.53 Sep-08 Call 1.4550 1.4675 0.0210 10.73% 0.6440 0.1060 25.29 12.12 Sep-08 Call 1.4600 1.4675 0.0178 10.60% 0.5901 0.1120 26.07 12.65 Sep-08 Call 1.4650 1.4675 0.0149 10.49% 0.5332 0.1160 26.40 12.94 Sep-08 Call 1.4700 1.4675 0.0123 10.40% 0.4747 0.1170 26.20 12.96 Sep-08 Call 1.4750 1.4675 0.0101 10.40% 0.4167 0.1150 25.68 12.71 Sep-08 Call 1.4800 1.4675 0.0081 10.30% 0.3592 0.1110 24.38 12.17 Sep-08 Call 1.4850 1.4675 0.0065 10.30% 0.3058 0.1040 22.87 11.42 Sep-08 Call 1.4900 1.4675 0.0051 10.28% 0.2560 0.0960 20.95 10.48 Sep-08 Put 1.4550 1.4675 0.0085 10.72% 0.3548 0.1065 25.31 12.12 Sep-08 Put 1.4600 1.4675 0.0103 10.59% 0.4088 0.1124 26.09 12.65 Sep-08 Put 1.4650 1.4675 0.0124 10.49% 0.4657 0.1161 26.41 12.94 Sep-08 Put 1.4700 1.4675 0.0148 10.40% 0.5242 0.1174 26.20 12.96 Sep-08 Put 1.4750 1.4675 0.0176 10.39% 0.5823 0.1152 25.63 12.71 Sep-08 Put 1.4800 1.4675 0.0206 10.31% 0.6395 0.1112 24.35 12.18 Sep-08 Put 1.4850 1.4675 0.0240 10.33% 0.6926 0.1042 22.89 11.43 Dec-08 Call 1.4200 1.4605 0.0573 10.71% 0.6904 0.0407 9.55 27.78 Dec-08 Call 1.4300 1.4605 0.0506 10.63% 0.6483 0.0432 10.00 29.29 Dec-08 Call 1.4400 1.4605 0.0443 10.55% 0.6040 0.0453 10.32 30.47 Dec-08 Call 1.4500 1.4605 0.0384 10.45% 0.5579 0.0470 10.48 31.25 Dec-08 Call 1.4550 1.4605 0.0357 10.42% 0.5342 0.0474 10.54 31.49 Dec-08 Call 1.4600 1.4605 0.0331 10.39% 0.5104 0.0478 10.54 31.61 Dec-08 Call 1.4650 1.4605 0.0306 10.35% 0.4864 0.0480 10.51 31.62 Dec-08 Call 1.4700 1.4605 0.0283 10.34% 0.4625 0.0479 10.46 31.51 Dec-08 Call 1.4750 1.4605 0.0261 10.32% 0.4387 0.0476 10.37 31.29 Dec-08 Call 1.4800 1.4605 0.0240 10.30% 0.4150 0.0472 10.23 30.96 Dec-08 Call 1.4850 1.4605 0.0221 10.30% 0.3920 0.0465 10.09 30.52 Dec-08 Call 1.4900 1.4605 0.0203 10.30% 0.3693 0.0457 9.91 29.98 Dec-08 Call 1.4950 1.4605 0.0185 10.26% 0.3466 0.0449 9.66 29.33 Dec-08 Call 1.5000 1.4605 0.0169 10.25% 0.3248 0.0438 9.42 28.61 10 . cmegroup.com/fx “Greek” OPtion Statistics continued Month Put/Call Strike Future Price Prem-ium Implied Volatility Delta Gamma Theta Vega Dec-08 Put 1.4200 1.4605 0.0171 10.72% 0.3033 0.0407 9.74 27.78 Dec-08 Put 1.4250 1.4605 0.0186 10.66% 0.3237 0.0421 9.93 28.57 Dec-08 Put 1.4300 1.4605 0.0203 10.63% 0.3452 0.0432 10.13 29.29 Dec-08 Put 1.4350 1.4605 0.0220 10.57% 0.3668 0.0444 10.26 29.92 Dec-08 Put 1.4400 1.4605 0.0239 10.54% 0.3894 0.0454 10.39 30.46 Dec-08 Put 1.4450 1.4605 0.0259 10.50% 0.4123 0.0462 10.49 30.91 Dec-08 Put 1.4500 1.4605 0.0280 10.46% 0.4356 0.0469 10.54 31.25 Dec-08 Put 1.4550 1.4605 0.0302 10.41% 0.4592 0.0475 10.55 31.49 Dec-08 Put 1.4600 1.4605 0.0326 10.39% 0.4831 0.0478 10.55 31.61 Dec-08 Put 1.4650 1.4605 0.0351 10.36% 0.5070 0.0479 10.50 31.62 Dec-08 Put 1.4700 1.4605 0.0377 10.33% 0.5310 0.0479 10.41 31.51 Dec-08 Put 1.4750 1.4605 0.0405 10.32% 0.5548 0.0476 10.31 31.29 Dec-08 Put 1.4800 1.4605 0.0434 10.31% 0.5783 0.0472 10.16 30.96 Dec-08 Put 1.4850 1.4605 0.0464 10.29% 0.6016 0.0466 9.98 30.52 Dec-08 Put 1.4900 1.4605 0.0496 10.30% 0.6242 0.0457 9.79 29.98 Dec-08 Put 1.4950 1.4605 0.0528 10.27% 0.6467 0.0449 9.53 29.34 Dec-08 Put 1.5000 1.4605 0.0561 10.24% 0.6689 0.0439 9.23 28.60 Obviously, if the call buyer is making money at an accelerating rate and losing money at a decelerating rate, the call writer is experiencing the opposite results. Gamma tends to be highest when an option is at- or near-to-the-money. But gamma declines as an option trends in- or out-of-the-money. Notice that theta and vega are likewise greatest when the market is at- or reasonably near-to-the-money. These values decline when the option goes in- or out-of-the-money as discussed below.
Thus, convexity, as measured by gamma, works to the maximum benefit of the holder of at-the-money options. 11 As an option goes into-the-money, its delta gets higher. Option buyers (sellers) are making (losing) money at an accelerating rate. As an option goes out-of-the-money, its delta gets lower and lower. Option buyers (sellers) are losing (making) money at a decelerating rate.
Gamma measures the rate of this acceleration or deceleration. . Managing Currency Risks with Futures Options Theta measures time value decay or the expected decline in the option premium given a forward movement in time towards the ultimate expiration date of the option, holding all other variables (such as price, volatility, short-term rates) constant. Time value decay and the degree to which this decay or erosion might accelerate as the option approaches expiration may be identified by examining the change in the theta. Time value decay works to the benefit of the short but to the detriment of the long. The same options that have high thetas also have high gammas. Convexity as measured by gamma works to the detriment of the short and to the benefit of the long.
Nearthe-money options will have high thetas and high gammas. As expiration approaches, both theta (measuring time value decay) and gamma (measuring convexity) increase. For example, our December 2008 1.4600 call had a theta of 10.54. This suggests that over the course of 7 days, holding all else equal, the value of this call option may fall 10.54 ticks or $0.0011 from its value of $0.0331. In other words, its value is expected to decline to $0.0320.
Note that we are quoting a theta in ticks over the course of 7 calendar days. It is also common to quote a theta over the course of a single day. Thus, it becomes apparent that you “can’t have your cake and eat it too.” In other words, it is difficult, if not impossible, to benefit from both time value decay and convexity simultaneously. Theta measures the rate at which an option premium declines as time moves forward, i.e., time value decay. Time value decay benefits sellers to the detriment of buyers. Theta is a dynamic concept and may change dramatically as option expiration draws near.
At- or near-to-the-money options experience rapidly accelerating time value decay when expiration is close. Away-from-the-money options experience less time value decay as in-and out-of-the-money options have less time value than do comparable at- or near-the-money options. Thetas associated with moderately in- or out-of-the-money options may be relatively constant as expiration approaches signifying linear decay characteristics.
Deep in- or out-of-the-money options will have very little or perhaps no time value. Thus, the theta associated with an option whose strike is very much away from the money may “bottom-out” or reach zero well before expiration. At- or near-the-money options experience the greatest amount of time value decay, but also the greatest amount of convexity. Option traders have to decide whether the market is essentially stable (sell options) or volatile (buy options). Vega measures the expected change in the premium given a change in marketplace volatility.
Normally, vega is expressed as the change in the premium given a one percent (1.0%) movement in volatility. For example, our December 2008 1.4600 call had a vega of 31.61. This suggests that its premium of $0.0331 might fluctuate by 31.61 ticks or $0.0032 if volatility were to move by 1% from the current implied volatility of 10.39%. Vega measures the responsiveness of the option premium to rising or falling volatility. 12 . cmegroup.com/fx Vega tends to be greatest when the option is at- or reasonably nearto-the-money. In- and out-of-the-money options have generally lower vegas. However, this effect is not terribly great. Note that vega tends to fall, rather than rise, as a near-to-the-money option approaches expiration.
This is unlike the movement of theta and gamma, which rise as expiration draws near. Volatility and convexity are very similar properties. This can be understood when one considers that it is only when the market is moving, or when the market is volatile, that the effects of convexity are observed. Remember that when you buy an option, convexity works to your benefit no matter whether underlying price movements are favorable or not.
If the market moves against you, you lose money but at a decelerating rate. If the market moves with you, you make money at an accelerating rate. Thus, the prospect of rising volatility is generally accompanied by beneficial effects from convexity (at least from the long’s standpoint). Volatility (as measured by vega) and convexity (as measured by gamma) are closely related insofar as it is only when the market is volatile that the effects of convexity are observed. Earlier, we suggested that it is generally impossible to enter an option strategy in which both time value decay and convexity worked to your benefit simultaneously.
Paradoxically, it may be possible to find option strategies where the prospect of rising volatility and time value decay work for you simultaneously (although convexity will work against you). This is possible because vega falls as expiration approaches while theta and gamma rise. For example, one might buy a long-term option experiencing the ill effects of time value decay while selling a shorter-term option, which benefits from time value decay. The benefits associated with the short-term option will outweigh the 13 disadvantages associated with the longer-term option.
And, the strategy will generally benefit from the prospect of rising volatility, as the long-term option will have a higher vega than will the shortterm option. Putting It All Together - Options are strongly affected by the forces of price, time and volatility/convexity. (We often consider convexity and volatility to be one and the same property for reasons discussed above.) “Exotic” option statistics such as delta, gamma, theta and vega are quite useful in measuring the effects of these variables. As a general rule, when you buy an option or enter into a strategy using multiple options where you generally buy more than you sell, convexity and the prospect of rising volatility work to your benefit. Time value decay generally works against you in those situations.
When you sell options or enter into strategies where you are generally selling more options than you buy, convexity and the prospect of rising volatility will work against you although time value decay will work to your benefit. The key point is that these variables – price, time and volatility – do not operate independently one from the other. Price may generally be considered the most important of these variables and will tend to dictate whether time value decay is more or less important than convexity and rising volatility. One can use this information to good effect when formulating a hedging strategy using options. The factors that impact upon the option premium including price, time and volatility are interdependent.
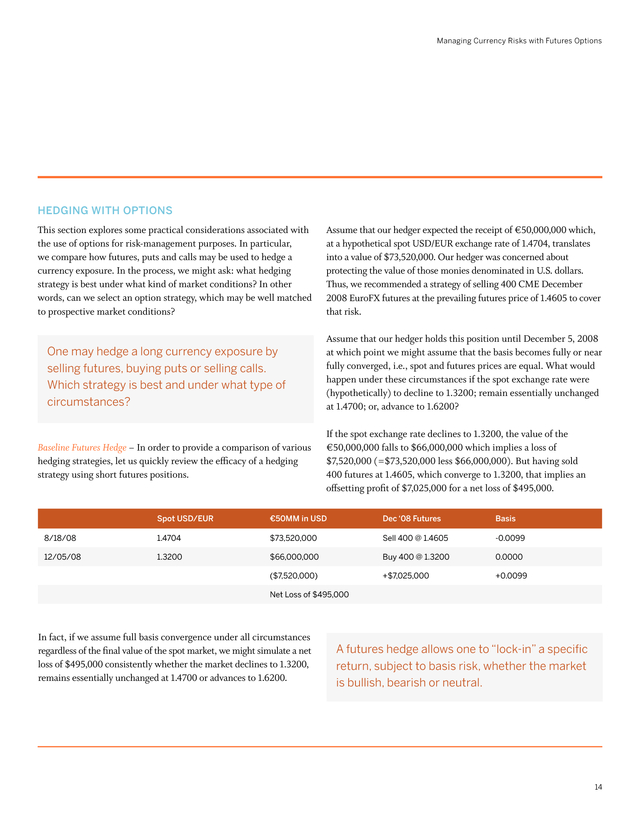
This has an important effect on the development of a speculative or a riskmanagement strategy with options. . Managing Currency Risks with Futures Options hedging with options This section explores some practical considerations associated with the use of options for risk-management purposes. In particular, we compare how futures, puts and calls may be used to hedge a currency exposure. In the process, we might ask: what hedging strategy is best under what kind of market conditions? In other words, can we select an option strategy, which may be well matched to prospective market conditions? One may hedge a long currency exposure by selling futures, buying puts or selling calls. Which strategy is best and under what type of circumstances? Baseline Futures Hedge – In order to provide a comparison of various hedging strategies, let us quickly review the efficacy of a hedging strategy using short futures positions. Assume that our hedger expected the receipt of €50,000,000 which, at a hypothetical spot USD/EUR exchange rate of 1.4704, translates into a value of $73,520,000. Our hedger was concerned about protecting the value of those monies denominated in U.S.
dollars. Thus, we recommended a strategy of selling 400 CME December 2008 EuroFX futures at the prevailing futures price of 1.4605 to cover that risk. Assume that our hedger holds this position until December 5, 2008 at which point we might assume that the basis becomes fully or near fully converged, i.e., spot and futures prices are equal. What would happen under these circumstances if the spot exchange rate were (hypothetically) to decline to 1.3200; remain essentially unchanged at 1.4700; or, advance to 1.6200? If the spot exchange rate declines to 1.3200, the value of the €50,000,000 falls to $66,000,000 which implies a loss of $7,520,000 (=$73,520,000 less $66,000,000). But having sold 400 futures at 1.4605, which converge to 1.3200, that implies an offsetting profit of $7,025,000 for a net loss of $495,000. Spot USD/EUR €50MM in USD Dec ‘08 Futures Basis 8/18/08 1.4704 $73,520,000 Sell 400 @ 1.4605 -0.0099 12/05/08 1.3200 $66,000,000 Buy 400 @ 1.3200 0.0000 ($7,520,000) +$7,025,000 +0.0099 Net Loss of $495,000 In fact, if we assume full basis convergence under all circumstances regardless of the final value of the spot market, we might simulate a net loss of $495,000 consistently whether the market declines to 1.3200, remains essentially unchanged at 1.4700 or advances to 1.6200. A futures hedge allows one to “lock-in” a specific return, subject to basis risk, whether the market is bullish, bearish or neutral. 14 .
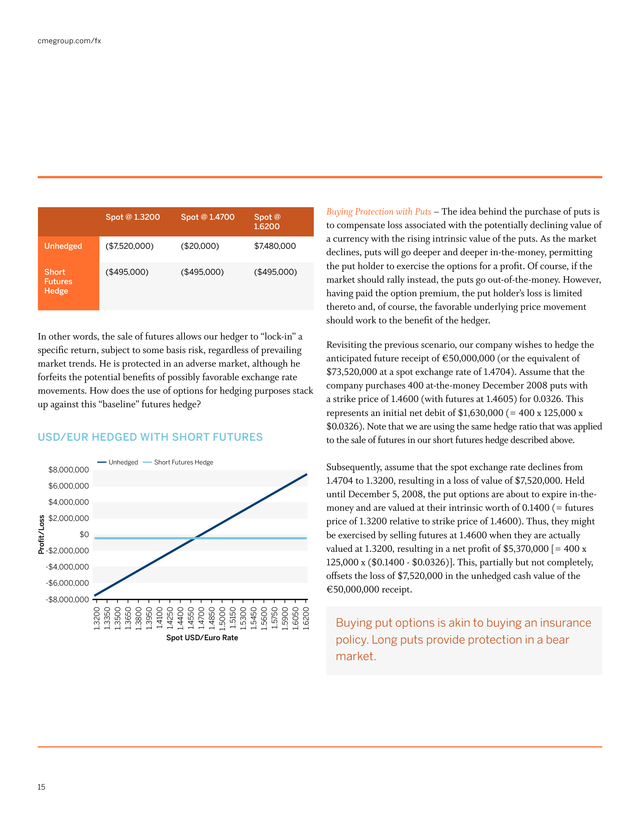
cmegroup.com/fx Spot @ 1.3200 Spot @ 1.4700 Spot @ 1.6200 Unhedged ($7,520,000) ($20,000) $7,480,000 Short Futures Hedge ($495,000) ($495,000) ($495,000) In other words, the sale of futures allows our hedger to “lock-in” a specific return, subject to some basis risk, regardless of prevailing market trends. He is protected in an adverse market, although he forfeits the potential benefits of possibly favorable exchange rate movements. How does the use of options for hedging purposes stack up against this “baseline” futures hedge? usd/eur hedged with short futures $8,000,000 Unhedged Short Futures Hedge $6,000,000 Proï¬t/Loss $4,000,000 $2,000,000 $0 -$2,000,000 -$4,000,000 -$6,000,000 1.3200 1.3350 1.3500 1.3650 1.3800 1.3950 1.4100 1.4250 1.4400 1.4550 1.4700 1.4850 1.5000 1.5150 1.5300 1.5450 1.5600 1.5750 1.5900 1.6050 1.6200 -$8,000,000 Spot USD/Euro Rate 15 Buying Protection with Puts – The idea behind the purchase of puts is to compensate loss associated with the potentially declining value of a currency with the rising intrinsic value of the puts. As the market declines, puts will go deeper and deeper in-the-money, permitting the put holder to exercise the options for a profit.
Of course, if the market should rally instead, the puts go out-of-the-money. However, having paid the option premium, the put holder’s loss is limited thereto and, of course, the favorable underlying price movement should work to the benefit of the hedger. Revisiting the previous scenario, our company wishes to hedge the anticipated future receipt of €50,000,000 (or the equivalent of $73,520,000 at a spot exchange rate of 1.4704). Assume that the company purchases 400 at-the-money December 2008 puts with a strike price of 1.4600 (with futures at 1.4605) for 0.0326.
This represents an initial net debit of $1,630,000 (= 400 x 125,000 x $0.0326). Note that we are using the same hedge ratio that was applied to the sale of futures in our short futures hedge described above. Subsequently, assume that the spot exchange rate declines from 1.4704 to 1.3200, resulting in a loss of value of $7,520,000. Held until December 5, 2008, the put options are about to expire in-themoney and are valued at their intrinsic worth of 0.1400 (= futures price of 1.3200 relative to strike price of 1.4600).
Thus, they might be exercised by selling futures at 1.4600 when they are actually valued at 1.3200, resulting in a net profit of $5,370,000 [= 400 x 125,000 x ($0.1400 - $0.0326)]. This, partially but not completely, offsets the loss of $7,520,000 in the unhedged cash value of the €50,000,000 receipt. Buying put options is akin to buying an insurance 15 policy. Long puts provide protection in a bear market. .
Managing Currency Risks with Futures Options Spot USD/EUR €50MM in USD Dec ‘08 Puts 8/18/08 1.4704 $73,520,000 Buy 400 1.4600 Puts @ 0.0326 12/05/08 1.3200 $66,000,000 Exercise 400 1.4600 Puts @ 0.1400 ($7,520,000) +$5,370,000 Net Loss of $2,150,000 Of course, if the spot market were to have remained essentially stable at 1.4700, then our hedger would have been left with slightly out-of-the-money and, therefore, worthless options by early December when expiration approached. Or, if the spot exchange rate had advanced, the hedger would likewise have essentially forfeited the initial $1,630,000 debit from the purchase of the 400 puts, but would have benefited from the market advance. A long put hedge allows you to lock-in a floor return while still retaining some upside potential. But if the market is neutral, one essentially forfeits the put premium paid up front. Spot @ 1.3200 Spot @ 1.4700 Spot @ 1.6200 Unhedged ($7,520,000) ($20,000) $7,480,000 Short Futures Hedge ($495,000) ($495,000) ($495,000) Long Put Hedge ($2,150,000) ($1,650,000) $5,850,000 As such, the long put hedge allows one to lock-in a floor return while still retaining a great deal of the upside potential associated with a possibly favorable market swing, limited to the extent that you pay the premium associated with the purchase of the put options up front. Option premiums are, of course, impacted by a variety of factors including the movement of price, time and volatility. So while the purchase of put options in the context of a hedging application reduces price risks, it also entails the acceptance of other types of risk uniquely applicable to options. Still, price impact is the foremost of these factors. 16 .
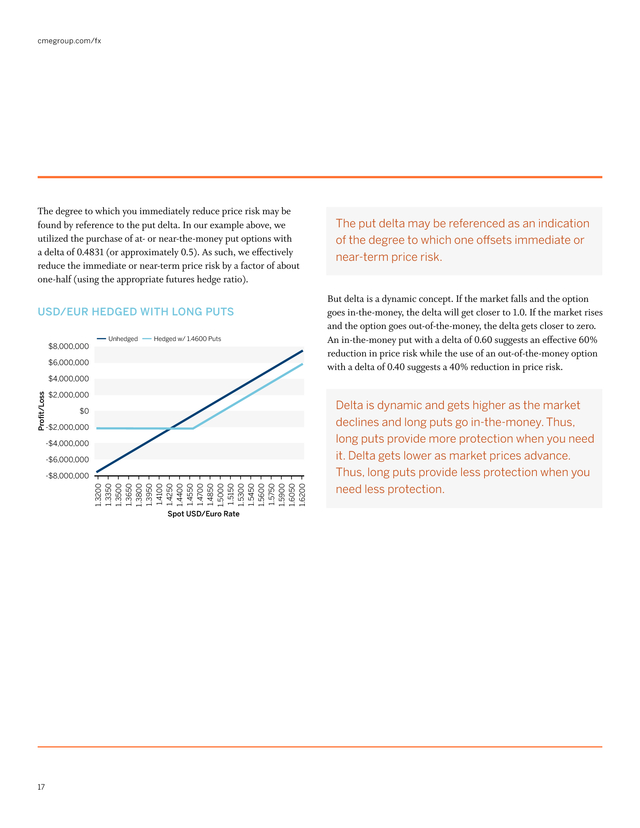
cmegroup.com/fx The degree to which you immediately reduce price risk may be found by reference to the put delta. In our example above, we utilized the purchase of at- or near-the-money put options with a delta of 0.4831 (or approximately 0.5). As such, we effectively reduce the immediate or near-term price risk by a factor of about one-half (using the appropriate futures hedge ratio). usd/eur hedged with long puts $8,000,000 Unhedged Hedged w/ 1.4600 Puts $6,000,000 The put delta may be referenced as an indication of the degree to which one offsets immediate or near-term price risk. But delta is a dynamic concept. If the market falls and the option goes in-the-money, the delta will get closer to 1.0.
If the market rises and the option goes out-of-the-money, the delta gets closer to zero. An in-the-money put with a delta of 0.60 suggests an effective 60% reduction in price risk while the use of an out-of-the-money option with a delta of 0.40 suggests a 40% reduction in price risk. Proï¬t/Loss $4,000,000 $2,000,000 $0 -$2,000,000 -$4,000,000 -$6,000,000 1.3200 1.3350 1.3500 1.3650 1.3800 1.3950 1.4100 1.4250 1.4400 1.4550 1.4700 1.4850 1.5000 1.5150 1.5300 1.5450 1.5600 1.5750 1.5900 1.6050 1.6200 -$8,000,000 Spot USD/Euro Rate 17 Delta is dynamic and gets higher as the market declines and long puts go in-the-money. Thus, long puts provide more protection when you need it. Delta gets lower as market prices advance. Thus, long puts provide less protection when you need less protection. .
Managing Currency Risks with Futures Options The dynamic nature of delta represents convexity. Convexity benefits the holder of a put insofar as it promises more protection in a bear market when you need more protection; and, less protection in a bull market when you would prefer less protection. Unfortunately, you pay for convexity by accepting negative time value decay. As expiration approaches, a near-to-the-money option will exhibit more and more time value decay or “accelerating” time value decay, or erosion.
It is interesting that the same options which experience high and rising convexity (near-term, near-the-moneys) also experience high and rising thetas. Barring a mispricing, it is impossible to experience both a positive gamma and theta when trading options. Yield Enhancement with Calls – If you believe that the market is basically stable, you might pursue a “yield enhancement” or “income augmentation” strategy by selling call options against a long cash or spot position. This is also known as “covered call writing,” in the sense that your obligation to deliver the underlying currency or futures contract, as a result of writing a call, is “covered” by the fact that you already own the currency or futures contract. The sale of calls against a long cash or spot exposure is often referred to as “covered call writing.” This strategy allows you to take advantage of an essentially neutral forecast. Thus, you must ask yourself … is the market basically volatile and, therefore, should you take advantage of convexity by buying options? Or, is the market essentially stable, recommending a strategy of taking advantage of time value decay by selling options? The purchase of puts as a hedging strategy implies that you believe that the market is volatile and want to take advantage of convexity. Revisiting the previous example, our company anticipates the receipt of €50,000,000 ($73,520,000 at a spot exchange rate of 1.4704).
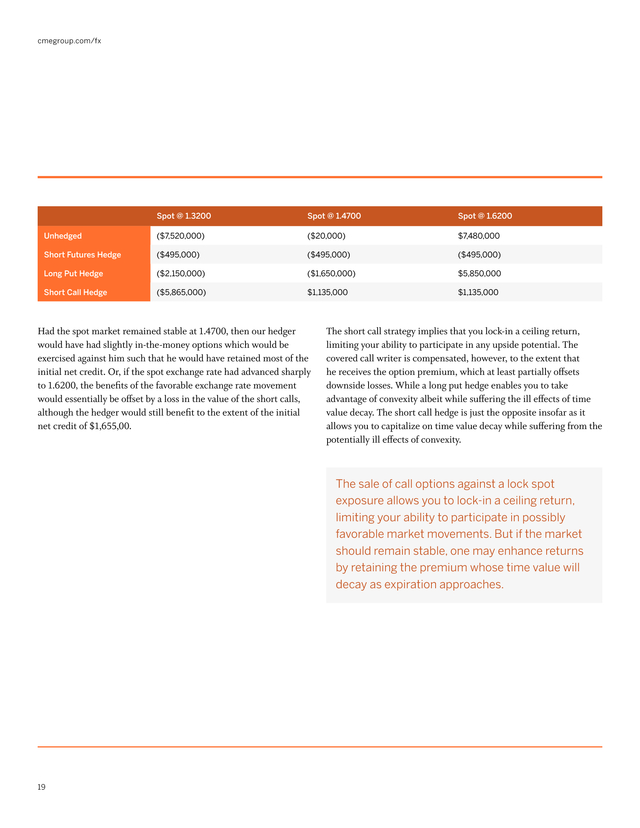
Assume that the company sells 400 at-the-money December 2008 calls with a strike price of 1.4600 (with futures at 1.4605) for 0.0331. This represents an initial net credit or receipt of cash of $1,655,000 (= 400 x 125,000 x $0.0331). Again, we employ the same hedge ratio that was applied to the short futures or long put hedges. Assume that spot exchange rates fall from 1.4704 to 1.3200 for a loss of $7,520,000.
Held until December 5, 2008, the 1.4600 calls options are out-of the-money, valued at zero and therefore abandoned. Thus, our hedger retains the $1,655,000 to at least partially offset the loss of $7,520,000 … or a net loss of $5,865,000. Spot USD/EUR €50MM in USD Dec ‘08 Calls 8/18/08 1.4704 $73,520,000 Sell 400 1.4600 Calls @ 0.0331 12/05/08 1.3200 $66,000,000 Abandon 400 1.4600 Calls @ 0.0000 ($7,520,000) +$1,655,000 Net Loss of $5,865,000 18 . cmegroup.com/fx Spot @ 1.3200 Spot @ 1.4700 Spot @ 1.6200 Unhedged ($7,520,000) ($20,000) $7,480,000 Short Futures Hedge ($495,000) ($495,000) ($495,000) Long Put Hedge ($2,150,000) ($1,650,000) $5,850,000 Short Call Hedge ($5,865,000) $1,135,000 $1,135,000 Had the spot market remained stable at 1.4700, then our hedger would have had slightly in-the-money options which would be exercised against him such that he would have retained most of the initial net credit. Or, if the spot exchange rate had advanced sharply to 1.6200, the benefits of the favorable exchange rate movement would essentially be offset by a loss in the value of the short calls, although the hedger would still benefit to the extent of the initial net credit of $1,655,00. The short call strategy implies that you lock-in a ceiling return, limiting your ability to participate in any upside potential. The covered call writer is compensated, however, to the extent that he receives the option premium, which at least partially offsets downside losses. While a long put hedge enables you to take advantage of convexity albeit while suffering the ill effects of time value decay.
The short call hedge is just the opposite insofar as it allows you to capitalize on time value decay while suffering from the potentially ill effects of convexity. The sale of call options against a lock spot exposure allows you to lock-in a ceiling return, limiting your ability to participate in possibly favorable market movements. But if the market should remain stable, one may enhance returns by retaining the premium whose time value will decay as expiration approaches. 19 . Managing Currency Risks with Futures Options usd/eur hedged with short calls $8,000,000 Unhedged Hedged w/ 1.4600 Calls $6,000,000 In- and Out-of-the-Money Options – Thus far, we have focused on the use of at- or at least near-to-the-money options in the context of our hedging strategies. But let us consider the use of in- and out-of-themoney long puts or short calls as an alternative. $4,000,000 Proï¬t/Loss The short call hedge works best when the market remains basically stable. In this case, time value decay results in a gradual decline in the premium. Thus, you “capture” the premium, enhancing yield. $2,000,000 $0 -$2,000,000 -$4,000,000 -$6,000,000 1.3200 1.3350 1.3500 1.3650 1.3800 1.3950 1.4100 1.4250 1.4400 1.4550 1.4700 1.4850 1.5000 1.5150 1.5300 1.5450 1.5600 1.5750 1.5900 1.6050 1.6200 -$8,000,000 Spot USD/Euro Rate Convexity and volatility are closely related concepts.
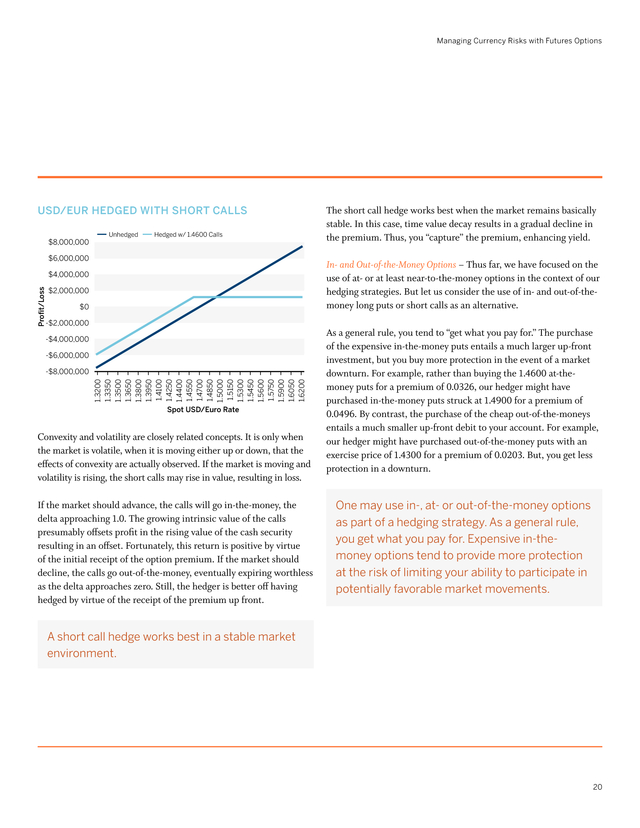
It is only when the market is volatile, when it is moving either up or down, that the effects of convexity are actually observed. If the market is moving and volatility is rising, the short calls may rise in value, resulting in loss. If the market should advance, the calls will go in-the-money, the delta approaching 1.0. The growing intrinsic value of the calls presumably offsets profit in the rising value of the cash security resulting in an offset.
Fortunately, this return is positive by virtue of the initial receipt of the option premium. If the market should decline, the calls go out-of-the-money, eventually expiring worthless as the delta approaches zero. Still, the hedger is better off having hedged by virtue of the receipt of the premium up front. As a general rule, you tend to “get what you pay for.” The purchase of the expensive in-the-money puts entails a much larger up-front investment, but you buy more protection in the event of a market downturn.
For example, rather than buying the 1.4600 at-themoney puts for a premium of 0.0326, our hedger might have purchased in-the-money puts struck at 1.4900 for a premium of 0.0496. By contrast, the purchase of the cheap out-of-the-moneys entails a much smaller up-front debit to your account. For example, our hedger might have purchased out-of-the-money puts with an exercise price of 1.4300 for a premium of 0.0203.
But, you get less protection in a downturn. One may use in-, at- or out-of-the-money options as part of a hedging strategy. As a general rule, you get what you pay for. Expensive in-themoney options tend to provide more protection at the risk of limiting your ability to participate in potentially favorable market movements. A short call hedge works best in a stable market environment. 20 .
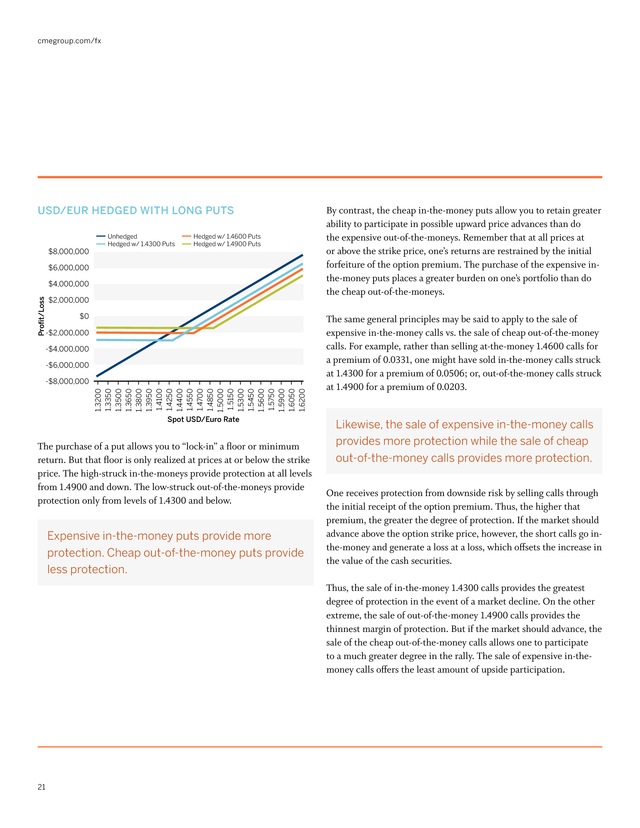
cmegroup.com/fx usd/eur hedged with Long puts $8,000,000 Unhedged Hedged w/ 1.4300 Puts Hedged w/ 1.4600 Puts Hedged w/ 1.4900 Puts $6,000,000 Proï¬t/Loss $4,000,000 $2,000,000 $0 -$2,000,000 -$4,000,000 -$6,000,000 1.3200 1.3350 1.3500 1.3650 1.3800 1.3950 1.4100 1.4250 1.4400 1.4550 1.4700 1.4850 1.5000 1.5150 1.5300 1.5450 1.5600 1.5750 1.5900 1.6050 1.6200 -$8,000,000 Spot USD/Euro Rate The purchase of a put allows you to “lock-in” a floor or minimum return. But that floor is only realized at prices at or below the strike price. The high-struck in-the-moneys provide protection at all levels from 1.4900 and down. The low-struck out-of-the-moneys provide protection only from levels of 1.4300 and below. Expensive in-the-money puts provide more protection.
Cheap out-of-the-money puts provide less protection. By contrast, the cheap in-the-money puts allow you to retain greater ability to participate in possible upward price advances than do the expensive out-of-the-moneys. Remember that at all prices at or above the strike price, one’s returns are restrained by the initial forfeiture of the option premium. The purchase of the expensive inthe-money puts places a greater burden on one’s portfolio than do the cheap out-of-the-moneys. The same general principles may be said to apply to the sale of expensive in-the-money calls vs.
the sale of cheap out-of-the-money calls. For example, rather than selling at-the-money 1.4600 calls for a premium of 0.0331, one might have sold in-the-money calls struck at 1.4300 for a premium of 0.0506; or, out-of-the-money calls struck at 1.4900 for a premium of 0.0203. Likewise, the sale of expensive in-the-money calls provides more protection while the sale of cheap out-of-the-money calls provides more protection. One receives protection from downside risk by selling calls through the initial receipt of the option premium. Thus, the higher that premium, the greater the degree of protection.
If the market should advance above the option strike price, however, the short calls go inthe-money and generate a loss at a loss, which offsets the increase in the value of the cash securities. Thus, the sale of in-the-money 1.4300 calls provides the greatest degree of protection in the event of a market decline. On the other extreme, the sale of out-of-the-money 1.4900 calls provides the thinnest margin of protection. But if the market should advance, the sale of the cheap out-of-the-money calls allows one to participate to a much greater degree in the rally.
The sale of expensive in-themoney calls offers the least amount of upside participation. 21 . Managing Currency Risks with Futures Options usd/eur hedged with short Calls $8,000,000 Unhedged Hedged w/ 1.4300 Calls Hedged w/ 1.4600 Calls Hedged w/ 1.4900 Calls $6,000,000 Proï¬t/Loss $4,000,000 $2,000,000 Matching Strategy with Forecast – Note that by buying puts against a long cash portfolio, the risk/reward profile associated with the entire position strongly resembles that of an outright long call. As such, this strategy is sometimes referred to as a “synthetic long call.” Likewise, the combination of selling calls against a long securities portfolio will strongly resemble the outright sale of a put. Thus, we sometimes refer to this strategy as a “synthetic short put.” $0 A prudent hedger may try to match his price forecast with the most beneficial hedging strategy. -$2,000,000 -$4,000,000 -$6,000,000 1.3200 1.3350 1.3500 1.3650 1.3800 1.3950 1.4100 1.4250 1.4400 1.4550 1.4700 1.4850 1.5000 1.5150 1.5300 1.5450 1.5600 1.5750 1.5900 1.6050 1.6200 -$8,000,000 Spot USD/Euro Rate Note, however, that the sale of calls options against a long spot position generally is considered a neutral strategy. One sells options to capitalize on time value decay in a stagnant market environment. Clearly, the sale of the at-the-moneys generates the most attractive return when yields remain stable.
This makes sense as the atthe-moneys have the greatest amount of time value to begin and experience the greatest degree of time value decay, as evidenced by their generally high thetas. Many textbooks draw a strong distinction between hedging or riskmanagement and speculative activity. We are not so sure that this distinction is warranted. Obviously, the same factors that might motivate a speculator to buy calls might motivate a hedger to buy puts against his cash portfolio.
And, the same factors that might motivate a speculator to sell puts might motivate a hedger to sell calls against his cash portfolio. How might we define hedging vs. speculative activity? Clearly a speculator is someone who might use futures and options in an attempt to make money. A hedger is someone who might use futures and options selectively in an attempt to make money and who already holds a cash position.
Perhaps this distinction is a bit cynical. It is, however, thoroughly practical. It is sometimes difficult to distinguish between speculation and “selective” hedging. 22 . cmegroup.com/fx The conclusion which might be reached from this discussion is that the necessity of making a price forecast is just as relevant from the hedger’s viewpoint as it is from the speculator’s viewpoint. Which one of our three basic hedge strategies: sell futures, buy puts or sell calls, is best? Clearly, that depends upon the market circumstances. In a bearish environment, where the holder of a cash portfolio needs to hedge the most, the alternative of selling futures is clearly superior to that of buying puts or selling calls. In a neutral environment, the sale of calls is superior, followed by the sale of futures and the purchase of puts. The best alternative in a bull market is simply not to hedge.
However, if one must attempt to limit risk, the best hedge alternative is to purchase of puts, followed by the sale of calls and the sale of futures. Matching Hedging Strategy with Forecast Bearish Neutral Bullish 1 Sell Futures Sell Calls Buy Puts 2 Buy Puts Sell Futures Sell Calls 3 Sell Calls Buy Puts Sell Futures Note that no single strategy is systematically or inherently superior to any other. Each achieves a number 1, 2 and 3 ranking, underscoring the speculative element in hedging. 23 A short futures hedge works best in a very bearish market environment. A long put hedge provides a good measure of downside protection but preserves one’s ability to benefit from a possibly favorable market advance.
Finally, a short call hedge is recommended in a neutral market environment. Collar Strategy – The concept of a long put hedge is very appealing to the extent that it provides limited downside risk while retaining at least a partial ability to participate in potential upside price movement. The problem with buying put options is, of course, the necessity to actually pay for the premium. Thus, some strategists have looked to strategies, which might at least partially offset the cost associated with the purchase of put options. One might, for example, combine the purchase of put options with the sale of call options.
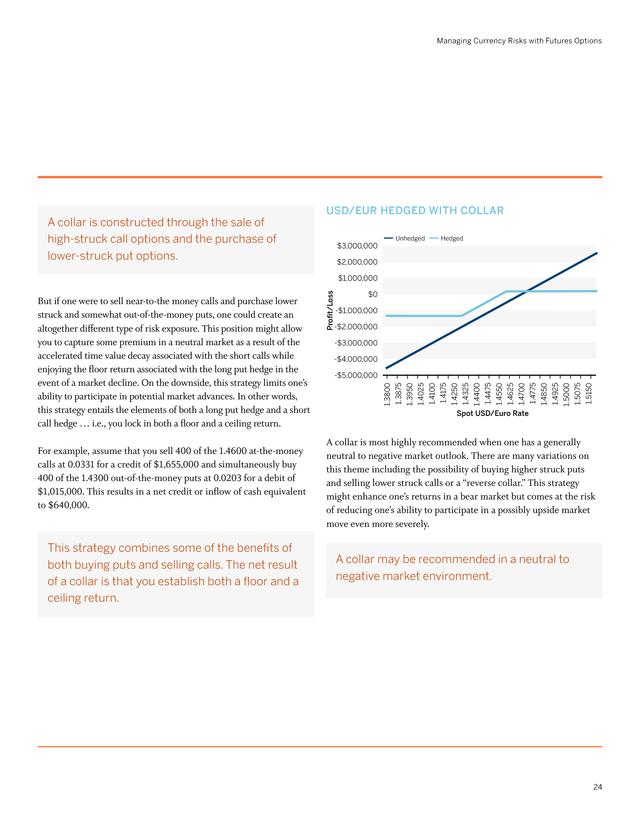
If one were to buy puts and sell calls at the same strike price, the resulting risks and returns would strongly resemble that of a short futures position. As a result, the combination of long puts and short calls at the same strike price is often referred to as a “synthetic short futures position.” Barring a market mispricing, however, there is no apparent advantage to assuming a synthetic as opposed to an actual futures position as part of a hedging strategy. . Managing Currency Risks with Futures Options A collar is constructed through the sale of high-struck call options and the purchase of lower-struck put options. usd/eur hedged with Collar Unhedged $3,000,000 Hedged $2,000,000 For example, assume that you sell 400 of the 1.4600 at-the-money calls at 0.0331 for a credit of $1,655,000 and simultaneously buy 400 of the 1.4300 out-of-the-money puts at 0.0203 for a debit of $1,015,000. This results in a net credit or inflow of cash equivalent to $640,000. This strategy combines some of the benefits of both buying puts and selling calls. The net result of a collar is that you establish both a floor and a ceiling return. $0 -$1,000,000 -$2,000,000 -$3,000,000 -$4,000,000 1.5150 1.5075 1.4925 1.5000 1.4775 1.4850 1.4625 1.4700 1.4475 1.4550 1.4325 1.4400 1.4175 1.4250 1.4100 1.4025 1.3875 1.3950 -$5,000,000 1.3800 But if one were to sell near-to-the money calls and purchase lower struck and somewhat out-of-the-money puts, one could create an altogether different type of risk exposure. This position might allow you to capture some premium in a neutral market as a result of the accelerated time value decay associated with the short calls while enjoying the floor return associated with the long put hedge in the event of a market decline.
On the downside, this strategy limits one’s ability to participate in potential market advances. In other words, this strategy entails the elements of both a long put hedge and a short call hedge … i.e., you lock in both a floor and a ceiling return. Proï¬t/Loss $1,000,000 Spot USD/Euro Rate A collar is most highly recommended when one has a generally neutral to negative market outlook. There are many variations on this theme including the possibility of buying higher struck puts and selling lower struck calls or a “reverse collar.” This strategy might enhance one’s returns in a bear market but comes at the risk of reducing one’s ability to participate in a possibly upside market move even more severely. A collar may be recommended in a neutral to negative market environment. 24 .
cmegroup.com/fx Delta Neutral Hedge – Options are extremely versatile instruments and there are many variations on the risk-management theme. In particular, it is always enticing to attempt to find a way to take advantage of the beneficial effects associated with options while minimizing the unfortunate effects that come as part of the package through a system of active management. Many of these systems rely upon the concept of delta as a central measure of risk and are known as “delta neutral” strategies. As an illustration, consider our hedger with the prospective receipt of €50,000,000 intent on hedging the risk of a falling euro vs. the U.S. dollar.
One might buy put options or sell call options against a long exposure with the intention of matching the net deltas. He may elect to sell 400 call options on EuroFX futures by reference to the futures hedge ratio. Or, the hedge may be weighted by reference to delta.
The appropriate “delta neutral hedge ratio” is readily determined by taking the reciprocal of the delta. A delta neutral hedging strategy calls for active management of an option position in such as way as to maintain a net delta near zero. 25 Delta Neutral Hedge Ratio = Futures Hedge Ratio ÷ Option Delta In our previous examples, we had considered the sale of 400 at-themoney 1.4600 call options with a delta of 0.5104. Employing a delta weighted strategy, the hedger might elect to utilize 828 options instead. Delta Neutral Hedge Ratio = Futures Hedge Ratio ÷ Option Delta = 400 ÷ 0.5104 = 784 options A delta neutral hedge ratio may be calculated by reference to the reciprocal of the option delta. But because delta is a dynamic concept, this strategy implies some rather active management. For example, as the market rallies and the calls go into-the-money, the call delta will start to increase, resulting in accelerating losses if no action is taken.
Thus, our hedger should reduce the size of the short call position as the market advances. For example, if the option delta advances from 0.5104 to 0.5500, this implies that the hedge ratio will decline to 727 positions (= 400 ÷ 0.5500). Thus, one might buy-back or liquidate some 57 positions as the market advances. .
Managing Currency Risks with Futures Options If you sell calls in a delta neutral manner, you may find it necessary to sell more calls as the market declines and liquidate calls as the market advances. If the market declines, the calls will go out-of-the-money and the call delta will fall. This too will result in accelerating net losses to the extent that the options will provide increasingly less protection as the market breaks. Thus, our hedger might sell more options on the way down. For example, if the call delta declines to 0.4800, this implies that the hedge ratio will advance to 833 positions (= 400 ÷ 0.4800). Thus, one might sell an additional 49 calls as the market declines. The application of a delta hedge strategy with the use of short calls implies an essentially neutral market forecast.
This is intuitive to the extent that the sale of call options implies that one wishes to take advantage of time value decay in an essentially sideways trending market environment. But sometimes the market does not cooperate. In particular, this strategy entails the risk of whipsaw markets, i.e., the possibility that one buys back positions on the way up and sells more on the way down. Thus, whipsaws may have you buying high and selling low as the market reverses from one direction to the other.
The perils of a whipsaw market imply that one might couple this strategy with a diligent effort in creating market forecasting tools specifically to avoid the ill effects of whipsaws. Instead of the use of call options as part of a delta neutral strategy, one might also consider the purchase of put options. A delta neutral hedging strategy entails the risk of whipsaw markets, i.e., the possibility that one is caught buying high and selling lows as part of the adjustment of the strategy. One might buy the at-the-money 1.4600 put options with a delta of 0.4831. Our formula suggests that one might utilize 828 options to neutralize one’s risk exposure as measured by delta. Delta Neutral Hedge Ratio = Futures Hedge Ratio ÷ Option Delta = 400 ÷ 0.4831 = 828 options 26 .
cmegroup.com/fx As was the case with our delta neutral short call hedge, we know that the put delta will be sensitive to changing market conditions. If, for example, the market were to decline, the puts will go intothe-money and the delta will increase. This implies that one might liquidate some of the long puts to maintain a delta neutral stance. Or, if the market advances, this implies that the put options may go out-of-the-money and the delta will decrease. This may suggest that you purchase more puts to maintain a delta neutral stance. However, one might observe that as the market declines, the put options essentially provide more protection just when you need it most by virtue of the advancing delta. Or, that the put options will provide less protection as the market advances by virtue of a declining delta at a point.
This calls the question … why adjust the hedge ratio when the options are “self-adjusting” in a beneficial way? Of course, the risk of this strategy is that the market might simply remain stagnant and the hedger is subject to the ill effects of time value decay. As such, the use of long options is a hedging strategy most aptly recommended in a volatile market environment. One may pursue a delta neutral strategy with the use of long put options. However, long puts are essentially self-adjusting in the sense that they provide more protection as the market moves adversely and less protection when the market moves favorably.
Thus, it is not clear whether one really needs to adjust the hedge ratio at all in this context. For more information on CME Group FX, visit www.cmegroup.com/fx. CME GROUP HEADQUARTERS 20 South Wacker Drive Chicago, Illinois 60606 cmegroup.com CME GROUP REGIONAL OFFICES info@cmegroup.com 800 331 3332 312 930 1000 New York 212 299 2000 London + 44 20 7796 7100 São Paulo Houston 713 658 9292 Washington D.C. 202 638 3838 +55 11 2565 5999 Singapore +65 6593 5555 Tokyo +81 3 5403 4828 Futures trading is not suitable for all investors, and involves the risk of loss. Futures are a leveraged investment, and because only a percentage of a contract’s value is required to trade, it is possible to lose more than the amount of money deposited for a futures position. Therefore, traders should only use funds that they can afford to lose without affecting their lifestyles.
And only a portion of those funds should be devoted to any one trade because they cannot expect to profit on every trade. All references to options refer to options on futures. CME Group is a trademark of CME Group Inc. The Globe Logo, CME, and Chicago Mercantile Exchange are trademarks of Chicago Mercantile Exchange Inc.
CBOT and the Chicago Board of Trade are trademarks of the Board of Trade of the City of Chicago, Inc. NYMEX is a registered trademark of the New York Mercantile Exchange, Inc. All other trademarks are the property of their respective owners. The information within this brochure has been compiled by CME Group for general purposes only.
CME Group assumes no responsibility for any errors or omissions. Additionally, all examples in this brochure are hypothetical situations, used for explanation purposes only, and should not be considered investment advice or the results of actual market experience. All matters pertaining to rules and specifications herein are made subject to and are superseded by official CME, CBOT and NYMEX rules.
Current rules should be consulted in all cases concerning contract specifications. Copyright © 2010 CME Group. All rights reserved. FX262/0/0410 .
These contracts are accessible through the CME Globex electronic trading platform. Exchange traded options are similar to exchange traded futures with respect to their relatively high degree of standardization. And like currency futures, trading volumes in options on currency futures have been growing very quickly in recent years. What is an Option? – Options provide a very flexible structure that may be tailor made to meet the risk management or speculative needs of the moment.
Options may generally be categorized as two types: calls and puts … with two very different risk/reward scenarios. 1 There are two types of options: call options and put options. Call options convey the right, but not the obligation, to buy a specified quantity currency at a particular strike or exercise price on or before an expiration date. One may either buy a call option, paying a negotiated price or premium to the seller, writer or grantor of the call; or, sell, write or grant a call, thereby receiving that premium. Put options convey the right, but not the obligation, to sell a specified quantity currency at a particular strike or exercise price on or before an expiration date.
Again, one may buy or sell a put option, either paying or receiving a negotiated premium or price. Buying a call is a bullish transaction; selling a call is bearish. Options may be configured as European- or American-style options. A European-style option may only be exercised on its expiration date while an American-style option may be exercised at any time up to and including the expiration date. We offer options on FX futures configured in both American- and European-styles. The purchase of a call option is an essentially bullish transaction with limited downside risk. If the market should advance above the strike price, the call is considered “in-the-money” and one may exercise the call by purchasing currency at the exercise price even when the exchange rate exceeds the exercise price.
This implies a profit that is diminished only by the premium paid up front to secure the option. If the market should decline below the strike price, the option is considered “out-of-the-money” and may expire, leaving the buyer with a loss limited to the premium. . Managing Currency Risks with Futures Options The risks and potential rewards, which accrue to the call seller or writer, are opposite that of the call buyer. If the option should expire out-of-the-money, the writer retains the premium and counts it as profit. If, the market should advance, the call writer is faced with the prospect of being forced to sell currency when the exchange rate is much higher, such losses cushioned to the extent of the premium received upon option sale. Profit/loss for call option Buy Put Option Sell Put Option Proï¬t Loss Buy Call Option Proï¬t Loss Sell Call Option Profit/loss for Put option Exchange Rate The purchase of a put option is essentially a bearish transaction with limited downside risk. If the market should decline below the strike price, the put is in-the-money and one may exercise the put by selling currency at the exercise price even when the exchange rate is less the exercise price.
If the market should advance above the strike price, the option is out-of-the-money, implying a loss equal to the premium. Buying a put is a bearish transaction while selling a put is a bullish transaction. Exchange Rate The risks and potential rewards, which accrue to the put writer, are opposite that of the put buyer. If the option should expire out-ofthe-money, the writer retains the premium and counts it as profit. If, the market should advance, the put writer is faced with the prospect of being forced to buy currency when the exchange rate is much lower, such losses cushioned to the extent of the premium received upon option sale. The purchase of an option implies limited risk and unlimited potential reward. The sale of an option implies limited reward and unlimited risk. 2 .
cmegroup.com/fx While one may dispose of an option through an exercise or abandonment (expiration without exercise), there is also the possibility that one may liquidate a long/short option through a subsequent sale/purchase. As such, option traders utilize a variety of mathematical pricing models to identify appropriate premium values not the least of which is the Black-Scholes option pricing model. Several factors including the relationship between market and exercise price, term until expiration, market volatility and interest rates impact the formula. Frequently, options are quoted in terms of volatility and converted into monetary terms with use of these formulae. Option buyers pay a premium to option sellers to compensate them for assuming these asymmetrical risks. Options are very flexible because they are available with many different expiration dates and strike prices. Specifications of Popular Options on FX Futures Options on EuroFX Futures Options on Japanese Yen Futures Options on British Pound Futures Options on Swiss Franc Futures Exercisable for One 125,000 euro futures contract One 12,500,000 yen futures contract One 62,500 pound futures contract One 125,000 franc futures contract Minimum Price Fluctuation (Tick) $0.0001 per euro ($12.50) $0.000001 per yen ($12.50) $0.0001 per pound ($6.25) $0.0001 per franc ($12.50) Price Limits None Strike Interval $0.005 per euro $0.00005 per yen $0.01 per pound $0.005 per franc Contract Months Four months in the March cycle (March, June, September and December) and two months not in the March cycle (serial months), plus 4 Weekly Expiration Options CME Globex® Trading Hours Mondays thru Thursdays from 5:00 pm to 4:00 pm the following day; Sundays and holidays from 3:00 pm – 4:00 pm the following day (Chicago Time) Trading Ends 2nd Friday before 3rd Wednesday of contract month (two Fridays ahead of the third Wednesday) The contracts in this piece are listed with, and subject to, the rules and regulations of CME. The “fair value” of an option is the price at which both buyer and seller might expect to break even if one were to randomly buy or sell options over a large number of trials. 3 .
Managing Currency Risks with Futures Options Because of the variety with which options are offered including puts and calls with varying exercise prices and expiration dates, one may create an almost infinite variety of strategies which may be tailored to suit one’s unique needs. Further, one deploys a combination of options to achieve particular risk management requirements. The intrinsic value of an option is equal to its in-the-money amount. If the option is out of the money, it has no intrinsic or in-the-money value. The intrinsic value is equivalent, and may be explained, by reference to the option’s “terminal value.” The terminal value of an option is the price the option would command just as it is about to expire. Option Pricing – Option pricing is at once one of the most complicated, but perhaps the most significant, topics that a prospective option trader can consider. The importance of being able to identify the “fair value” of an option is evident when you consider the meaning of the term “fair value” in the context of this subject. When an option is about to expire, an option holder has two alternatives available to him.
On one hand, the holder may elect to exercise the option or, on the other hand, may allow it to expire unexercised. Because the holder cannot continue to hold the option in the hopes that the premium will appreciate and the option may be sold for a profit, the option’s value is limited to whatever profit it may generate upon exercise. But how can a trader recognize over or under-priced options? What variables impact upon this assessment? There are a number of mathematical models, which may be used to calculate these figures, notably including models introduced by Black Scholes, Cox Ross Rubinstein and Whaley amongst others. The purpose of this section, however, is not to describe these models but to introduce some of the fundamental variables which impact upon an option premium and their effect.
Fundamentally, an option premium reflects two components: “intrinsic value” and “time value.” Intrinsic and time value of call Intrinsic Value Time Value Options Premium A fair market value for an option is such that the buyer and seller expect to break even in a statistical sense, i.e., over a large number of trials (without considering the effect of transaction costs, commissions, etc.). Thus, if a trader consistently buys over-priced or sells under-priced options, he can expect, over the long term, to incur a loss. By the same token, an astute trader who consistently buys under-priced and sells over-priced options might expect to realize a profit. Exchange Rate Premium = Intrinsic Value + Time Value A number of mathematical models are employed to identify the fair value of an option notably including the Black-Scholes model. An option premium is composed of its intrinsic or in-the-money value plus its time value or value beyond its intrinsic value. 4 .
cmegroup.com/fx As such, the issue revolves entirely on whether the option lies in-the-money or out-of-the-money as expiration draws near. If the option is out-of-the-money then, of course, it will be unprofitable to exercise and the holder will allow it to expire unexercised or “abandon” the option. An abandoned option is worthless and, therefore, the terminal value of an out-of-the-money option is zero. If the option is in-the-money, the holder will profit upon exercise by the in-the-money amount and, therefore, the terminal value of an in-the-money option equals the in-the-money amount. An option should (theoretically) never trade below its intrinsic value. If it did, then arbitrageurs would immediately buy all the options they could for less than the in-the-money amount, exercise the option and realize a profit equal to the difference between the in-the-money amount and the premium paid for the option. When an option is about to expire, it is either in-themoney and exercisable for a value reflected in the difference between market and strike price or, it is at- or out-of-the-money and has zero intrinsic value. Intrinsic and time value of put option Time Value Options Premium Intrinsic Value Exchange Rate 5 Theoretically, an option should never trade below its intrinsic value.
If it did, there would be an arbitrage opportunity that might soon be exploited, driving the premium up to its intrinsic value. Time Value – An option contract often trades at a level in excess of its intrinsic value. This excess is referred to as the option’s “time value” or sometimes as its “extrinsic value.” When an option is about to expire, its premium is reflective solely of intrinsic value. But when there is some time until option expiration, there exists some probability that market conditions will change such that the option may become profitable (or more profitable) to exercise.
Thus, time value reflects the probability of a favorable development in terms of prevailing market conditions, which might permit a profitable exercise. Generally, an option’s time value will be greatest when the option is at-the-money. In order to understand this point, consider options that are deep in- or out-of-the-money. When an option is deep out-of-the-money, the probability that the option will ever trade in-the-money becomes remote.
Thus, the option’s time value becomes negligible or even zero. An option may have value in excess of its intrinsic value. An option’s time value essentially represents the possibility that the option might go in-the-money in the future, thus permitting a profitable exercise. . Managing Currency Risks with Futures Options When an option trades deep in-the-money, the leverage associated with the option declines. Leverage is the ability to control a large amount of resources with a relatively modest investment. Consider the extraordinary case where a call option has a strike price of zero. Under these circumstances, the option’s intrinsic value equals the outright purchase price of the instrument. There is no leverage associated with this option and, therefore, the option trader might as well simply buy the underlying instrument outright.
Thus, there is no time value associated with the option. A number of different factors impact on an option on futures’ time value in addition to the in- or out-of-the-money amount. These include … (i) term until option expiration; (ii) market volatility; and (iii) short term interest rates. Options exercisable for actual commodities or financial instruments are also affected by any other cash flows such as dividends (in the case of stock), coupon payments (bonds), etc. In addition to the relationship between market and strike price, the premium of an option on a futures contract is also affected by the term until expiration, market volatility and short-term interest rates. Time Value Decay 2 Mths til Expiration Value at Expiration Time value decay or erosion tends to accelerate with respect to at- or near-to-the-money options. Not only will the time value of an option decline over time, but that time value “decay” or “erosion” may accelerate as the option approaches expiration.
But be aware that accelerating time value decay is a phenomenon that is characteristic of at- or near-themoney options only. Deep in- or out-of-the-money options tend to exhibit a linear pattern of time value decay. Options Premium 3 Mths til Expiration 1 Mths til Expiration Term until Expiration – An option’s extrinsic value is most often referred to as time value for the simple reason that the term until option expiration has perhaps the most significant and dramatic effect upon the option premium. All other things being equal, premiums will always diminish over time until option expiration. In order to understand this phenomenon, consider that options perform two basic functions – (i) they permit commercial interests to hedge or offset the risk of adverse price movement; and (ii) they permit traders to speculate on anticipated price movements. The first function suggests that options represent a form of price insurance.
The longer the term of any insurance policy, the more it costs. The longer the life of an option, the greater the probability that adverse events will occur … hence, the value of this insurance is greater. Likewise, when there is more time left until expiration, there is more time during which the option could potentially move in-the-money.
Therefore, speculators will pay more for an option with a longer life. Exchange Rate 6 . cmegroup.com/fx Volatility impacts an option’s time value to the extent that it measures the extent to which the underlying market price may fluctuate, possibly driving the option into-the-money. Volatility – Option holders can profit when options trend into the money. If currency values are expected to move upwards by 10%, option traders would become inclined to buy call options. But if currency values were expected to move upwards by 20% over the same time period, traders would become even more anxious to buy calls, bidding the premium up in the process. It is not always easy to predict the direction in which prices will move, but it may nonetheless be possible to measure volatility. Market volatility is often thought of as price movement in either direction, up or down. In this sense, it is the magnitude, not the direction, of the movement that counts. Standard deviation is a statistic that is often employed to measure volatility.
For example, you may see a volatility assessed at 10%, 15%, 20%, etc. The use of this statistic implies that commodity price movements may be modeled by the “normal price distribution.” The normal distribution is represented by the familiar bell shaped curve. To interpret a volatility of 19%, for example, you can say with approximately 68% certainty that the price of the underlying instrument will be within plus or minus 19% of where it is now at the conclusion of a year. Or, with a probability of 95%, that the price of the underlying instrument will be within plus or minus 38% (2 x 19%) of where the price lies now at the conclusion of a year.
A good rule of thumb is that the greater the price volatility, the more the option will be worth. 7 Volatility is typically measured by the annualized standard deviation of percentage movements in the underlying market price. Short Term Rates – Whenever someone invests in any venture some positive return typically is expected. Accordingly, when an option exercisable for a futures contract is purchased there is an investment equal to the premium. To the extent that the option is paid for up front and in cash, a return is expected on the investment.
This implies that premiums must be discounted to reflect the lost opportunity represented by an investment in options. When the opportunity cost rises, as reflected in the rate at which funds may alternately be invested on a short term basis, the price of an option is discounted accordingly. When the opportunity cost decreases, the premium appreciates. When you buy an option, you pay cash. Shortterm interest rates play a role in determining the option premium because they reflect the opportunity costs associated with committing that cash to options. These remarks must be qualified by the following considerations: First, the effect described is applicable only to options on futures and not to options exercisable for actual instruments.
In fact, rising short term rates will tend to increase call premiums and decrease put premiums for options exercisable for actual instruments. Secondly, these remarks apply holding all other considerations equal. But of course, we know that all else is never held equal. For example, if short term rates are rising or falling, this suggests that bond futures prices will be affected.
Of course, this consideration will also have an impact, often much greater in magnitude, than the impact of fluctuating short term rates. . Managing Currency Risks with Futures Options Delta – When the price of the underlying instrument rises, call premiums rise and put premiums fall. But by how much? The change in the premium relative to the change in the underlying commodity price is measured by a common option statistic known as “delta.” Delta is generally expressed as a number from zero to 1.0. Deep in-the-money deltas will approach 1.0. Deep out-of-the-money deltas will approach zero. Finally at- or near-the-money deltas will run at about 0.50. Delta Deep In-the-money ⇒ At-the-Money ⇒ Deep Out-of-the-Money ⇒ 1.00 0.50 0.00 It is easy to understand why a deep in- or out-of-the-money option may have a delta equal to 1.0 or zero, respectively.
A deep in-themoney premium is reflective solely of intrinsic or in-the-money value. If the option moves slightly more or less in-the-money, its time value may be unaffected. Its intrinsic value, however, reflects the relationship between the market price and the fixed strike price. Hence, a delta of 1.0. Movements in the price of the instrument for which an option may be exercised are probably the most significant factor impacting an option premium.
Delta measures the expected change in the premium given a change in the underlying market price. At the other extreme, a deep out-of-the-money option has no value and is completely unaffected by slightly fluctuating market prices. Hence, a delta of zero. A call delta of 0.50 suggests that if the value of the underlying instrument advances by $1, the premium will advance by 50 cents. A put delta of 0.50 suggests that if the value of the underlying instrument advances by $1, the premium will fall by 50 cents. Delta is measured on a scale from 0 to 1. Deep inthe-money options will have deltas that approach 1 while deep out-of-the-money options will have deltas that approach zero. At-the-money options will tend to have deltas near 0.5. Delta is a dynamic concept.
It will change as the market price moves upwards or downwards. Hence, if an at-the-money call starts trending into the money, its delta will start to climb. Or, if the market starts falling, the call delta will likewise fall. “Greek” Statistics – In addition to movement in the underlying market price (as measured by delta), other factors impact significantly upon the option premium, notably including time until expiration and marketplace volatility.
A number of exotic “Greek” statistics including delta, gamma, vega and theta are often referenced to measure the impact of these factors upon the option premium. Underlying price movement stands out as perhaps the most obvious factor impacting option premiums and we have already discussed delta as the measure of such impact. Let’s consider other statistics including gamma, vega and theta. 8 .
cmegroup.com/fx Option premiums respond to fluctuations with respect to price, time and volatility. A number of statistics including delta, gamma, theta and vega are referenced to measure the responsiveness of option premiums to these factors. Gamma may be thought of as the “delta of the delta.” Gamma measures the expected change in the delta given a change in the underlying market price. Gamma is said to measure a phenomenon known as “convexity.” Convexity refers to the shape of the curve, which depicts the total value of an option premium over a range in possible underlying market values. The curvature of that line is said to be convex, hence the term convexity. “Greek” OPtion Statistics Delta Measures the expected change in the option premium given a change in the PRICE of the instrument underlying the option Gamma Measures the change in the DELTA given a change in the PRICE of the instrument underlying the option, i.e., the “delta of the delta” measuring a phenomenon known as “Convexity” Vega Measures the expected change in the option premium given a change in VOLATILITY of the instrument underlying the option Theta Measures the expected change in the option premium given the forward movement of TIME Gamma is the “delta of the delta,” measuring the prospective change in the delta given a change in the underlying market price.
Gamma is said to measure “convexity.” Convexity is a concept, which promises to benefit traders who purchase options to the detriment of those who sell or write options. Consider that as the market rallies, the premium advances at an ever-increasing rate as the delta itself advances. Thus, the holder of a call is making money at an increasing or accelerating rate.
But if the market should fall, the call holder is losing money, but at a decelerating rate. 9 On August 18, 2008, for example, the delta for a December 2008 1.4600 call (essentially at-the-money with December futures trading at 1.4605) was 0.5104. It had a gamma of 0.0478 suggesting that if the underlying futures price were to move upwards (downwards) by 1 cent, the value of delta would move upwards (downwards) by about 0.0478. This may be validated by noting that the call struck at 1.4500 has a delta of 0.5579 or 0.0475 higher than 0.5104.
Or, that the call struck at 1.4700 has a delta of 0.4625 or 0.0479 lower than 0.5104. It is important to note that the gammas in our illustration are based upon a 1 cent or $0.01 movement in the EUR/USD exchange rate. The convexity property of options benefits option buyers to the detriment of option sellers. . Managing Currency Risks with Futures Options “Greek” OPtion Statistics Month Put/Call Strike Future Price Prem-ium Implied Volatility Delta Gamma Theta Vega Sep-08 Call 1.4400 1.4675 0.0320 11.07% 0.7819 0.0810 20.61 9.57 Sep-08 Call 1.4450 1.4675 0.0281 10.95% 0.7407 0.0910 22.41 10.53 Sep-08 Call 1.4550 1.4675 0.0210 10.73% 0.6440 0.1060 25.29 12.12 Sep-08 Call 1.4600 1.4675 0.0178 10.60% 0.5901 0.1120 26.07 12.65 Sep-08 Call 1.4650 1.4675 0.0149 10.49% 0.5332 0.1160 26.40 12.94 Sep-08 Call 1.4700 1.4675 0.0123 10.40% 0.4747 0.1170 26.20 12.96 Sep-08 Call 1.4750 1.4675 0.0101 10.40% 0.4167 0.1150 25.68 12.71 Sep-08 Call 1.4800 1.4675 0.0081 10.30% 0.3592 0.1110 24.38 12.17 Sep-08 Call 1.4850 1.4675 0.0065 10.30% 0.3058 0.1040 22.87 11.42 Sep-08 Call 1.4900 1.4675 0.0051 10.28% 0.2560 0.0960 20.95 10.48 Sep-08 Put 1.4550 1.4675 0.0085 10.72% 0.3548 0.1065 25.31 12.12 Sep-08 Put 1.4600 1.4675 0.0103 10.59% 0.4088 0.1124 26.09 12.65 Sep-08 Put 1.4650 1.4675 0.0124 10.49% 0.4657 0.1161 26.41 12.94 Sep-08 Put 1.4700 1.4675 0.0148 10.40% 0.5242 0.1174 26.20 12.96 Sep-08 Put 1.4750 1.4675 0.0176 10.39% 0.5823 0.1152 25.63 12.71 Sep-08 Put 1.4800 1.4675 0.0206 10.31% 0.6395 0.1112 24.35 12.18 Sep-08 Put 1.4850 1.4675 0.0240 10.33% 0.6926 0.1042 22.89 11.43 Dec-08 Call 1.4200 1.4605 0.0573 10.71% 0.6904 0.0407 9.55 27.78 Dec-08 Call 1.4300 1.4605 0.0506 10.63% 0.6483 0.0432 10.00 29.29 Dec-08 Call 1.4400 1.4605 0.0443 10.55% 0.6040 0.0453 10.32 30.47 Dec-08 Call 1.4500 1.4605 0.0384 10.45% 0.5579 0.0470 10.48 31.25 Dec-08 Call 1.4550 1.4605 0.0357 10.42% 0.5342 0.0474 10.54 31.49 Dec-08 Call 1.4600 1.4605 0.0331 10.39% 0.5104 0.0478 10.54 31.61 Dec-08 Call 1.4650 1.4605 0.0306 10.35% 0.4864 0.0480 10.51 31.62 Dec-08 Call 1.4700 1.4605 0.0283 10.34% 0.4625 0.0479 10.46 31.51 Dec-08 Call 1.4750 1.4605 0.0261 10.32% 0.4387 0.0476 10.37 31.29 Dec-08 Call 1.4800 1.4605 0.0240 10.30% 0.4150 0.0472 10.23 30.96 Dec-08 Call 1.4850 1.4605 0.0221 10.30% 0.3920 0.0465 10.09 30.52 Dec-08 Call 1.4900 1.4605 0.0203 10.30% 0.3693 0.0457 9.91 29.98 Dec-08 Call 1.4950 1.4605 0.0185 10.26% 0.3466 0.0449 9.66 29.33 Dec-08 Call 1.5000 1.4605 0.0169 10.25% 0.3248 0.0438 9.42 28.61 10 . cmegroup.com/fx “Greek” OPtion Statistics continued Month Put/Call Strike Future Price Prem-ium Implied Volatility Delta Gamma Theta Vega Dec-08 Put 1.4200 1.4605 0.0171 10.72% 0.3033 0.0407 9.74 27.78 Dec-08 Put 1.4250 1.4605 0.0186 10.66% 0.3237 0.0421 9.93 28.57 Dec-08 Put 1.4300 1.4605 0.0203 10.63% 0.3452 0.0432 10.13 29.29 Dec-08 Put 1.4350 1.4605 0.0220 10.57% 0.3668 0.0444 10.26 29.92 Dec-08 Put 1.4400 1.4605 0.0239 10.54% 0.3894 0.0454 10.39 30.46 Dec-08 Put 1.4450 1.4605 0.0259 10.50% 0.4123 0.0462 10.49 30.91 Dec-08 Put 1.4500 1.4605 0.0280 10.46% 0.4356 0.0469 10.54 31.25 Dec-08 Put 1.4550 1.4605 0.0302 10.41% 0.4592 0.0475 10.55 31.49 Dec-08 Put 1.4600 1.4605 0.0326 10.39% 0.4831 0.0478 10.55 31.61 Dec-08 Put 1.4650 1.4605 0.0351 10.36% 0.5070 0.0479 10.50 31.62 Dec-08 Put 1.4700 1.4605 0.0377 10.33% 0.5310 0.0479 10.41 31.51 Dec-08 Put 1.4750 1.4605 0.0405 10.32% 0.5548 0.0476 10.31 31.29 Dec-08 Put 1.4800 1.4605 0.0434 10.31% 0.5783 0.0472 10.16 30.96 Dec-08 Put 1.4850 1.4605 0.0464 10.29% 0.6016 0.0466 9.98 30.52 Dec-08 Put 1.4900 1.4605 0.0496 10.30% 0.6242 0.0457 9.79 29.98 Dec-08 Put 1.4950 1.4605 0.0528 10.27% 0.6467 0.0449 9.53 29.34 Dec-08 Put 1.5000 1.4605 0.0561 10.24% 0.6689 0.0439 9.23 28.60 Obviously, if the call buyer is making money at an accelerating rate and losing money at a decelerating rate, the call writer is experiencing the opposite results. Gamma tends to be highest when an option is at- or near-to-the-money. But gamma declines as an option trends in- or out-of-the-money. Notice that theta and vega are likewise greatest when the market is at- or reasonably near-to-the-money. These values decline when the option goes in- or out-of-the-money as discussed below.
Thus, convexity, as measured by gamma, works to the maximum benefit of the holder of at-the-money options. 11 As an option goes into-the-money, its delta gets higher. Option buyers (sellers) are making (losing) money at an accelerating rate. As an option goes out-of-the-money, its delta gets lower and lower. Option buyers (sellers) are losing (making) money at a decelerating rate.
Gamma measures the rate of this acceleration or deceleration. . Managing Currency Risks with Futures Options Theta measures time value decay or the expected decline in the option premium given a forward movement in time towards the ultimate expiration date of the option, holding all other variables (such as price, volatility, short-term rates) constant. Time value decay and the degree to which this decay or erosion might accelerate as the option approaches expiration may be identified by examining the change in the theta. Time value decay works to the benefit of the short but to the detriment of the long. The same options that have high thetas also have high gammas. Convexity as measured by gamma works to the detriment of the short and to the benefit of the long.
Nearthe-money options will have high thetas and high gammas. As expiration approaches, both theta (measuring time value decay) and gamma (measuring convexity) increase. For example, our December 2008 1.4600 call had a theta of 10.54. This suggests that over the course of 7 days, holding all else equal, the value of this call option may fall 10.54 ticks or $0.0011 from its value of $0.0331. In other words, its value is expected to decline to $0.0320.
Note that we are quoting a theta in ticks over the course of 7 calendar days. It is also common to quote a theta over the course of a single day. Thus, it becomes apparent that you “can’t have your cake and eat it too.” In other words, it is difficult, if not impossible, to benefit from both time value decay and convexity simultaneously. Theta measures the rate at which an option premium declines as time moves forward, i.e., time value decay. Time value decay benefits sellers to the detriment of buyers. Theta is a dynamic concept and may change dramatically as option expiration draws near.
At- or near-to-the-money options experience rapidly accelerating time value decay when expiration is close. Away-from-the-money options experience less time value decay as in-and out-of-the-money options have less time value than do comparable at- or near-the-money options. Thetas associated with moderately in- or out-of-the-money options may be relatively constant as expiration approaches signifying linear decay characteristics.
Deep in- or out-of-the-money options will have very little or perhaps no time value. Thus, the theta associated with an option whose strike is very much away from the money may “bottom-out” or reach zero well before expiration. At- or near-the-money options experience the greatest amount of time value decay, but also the greatest amount of convexity. Option traders have to decide whether the market is essentially stable (sell options) or volatile (buy options). Vega measures the expected change in the premium given a change in marketplace volatility.
Normally, vega is expressed as the change in the premium given a one percent (1.0%) movement in volatility. For example, our December 2008 1.4600 call had a vega of 31.61. This suggests that its premium of $0.0331 might fluctuate by 31.61 ticks or $0.0032 if volatility were to move by 1% from the current implied volatility of 10.39%. Vega measures the responsiveness of the option premium to rising or falling volatility. 12 . cmegroup.com/fx Vega tends to be greatest when the option is at- or reasonably nearto-the-money. In- and out-of-the-money options have generally lower vegas. However, this effect is not terribly great. Note that vega tends to fall, rather than rise, as a near-to-the-money option approaches expiration.
This is unlike the movement of theta and gamma, which rise as expiration draws near. Volatility and convexity are very similar properties. This can be understood when one considers that it is only when the market is moving, or when the market is volatile, that the effects of convexity are observed. Remember that when you buy an option, convexity works to your benefit no matter whether underlying price movements are favorable or not.
If the market moves against you, you lose money but at a decelerating rate. If the market moves with you, you make money at an accelerating rate. Thus, the prospect of rising volatility is generally accompanied by beneficial effects from convexity (at least from the long’s standpoint). Volatility (as measured by vega) and convexity (as measured by gamma) are closely related insofar as it is only when the market is volatile that the effects of convexity are observed. Earlier, we suggested that it is generally impossible to enter an option strategy in which both time value decay and convexity worked to your benefit simultaneously.
Paradoxically, it may be possible to find option strategies where the prospect of rising volatility and time value decay work for you simultaneously (although convexity will work against you). This is possible because vega falls as expiration approaches while theta and gamma rise. For example, one might buy a long-term option experiencing the ill effects of time value decay while selling a shorter-term option, which benefits from time value decay. The benefits associated with the short-term option will outweigh the 13 disadvantages associated with the longer-term option.
And, the strategy will generally benefit from the prospect of rising volatility, as the long-term option will have a higher vega than will the shortterm option. Putting It All Together - Options are strongly affected by the forces of price, time and volatility/convexity. (We often consider convexity and volatility to be one and the same property for reasons discussed above.) “Exotic” option statistics such as delta, gamma, theta and vega are quite useful in measuring the effects of these variables. As a general rule, when you buy an option or enter into a strategy using multiple options where you generally buy more than you sell, convexity and the prospect of rising volatility work to your benefit. Time value decay generally works against you in those situations.
When you sell options or enter into strategies where you are generally selling more options than you buy, convexity and the prospect of rising volatility will work against you although time value decay will work to your benefit. The key point is that these variables – price, time and volatility – do not operate independently one from the other. Price may generally be considered the most important of these variables and will tend to dictate whether time value decay is more or less important than convexity and rising volatility. One can use this information to good effect when formulating a hedging strategy using options. The factors that impact upon the option premium including price, time and volatility are interdependent.
This has an important effect on the development of a speculative or a riskmanagement strategy with options. . Managing Currency Risks with Futures Options hedging with options This section explores some practical considerations associated with the use of options for risk-management purposes. In particular, we compare how futures, puts and calls may be used to hedge a currency exposure. In the process, we might ask: what hedging strategy is best under what kind of market conditions? In other words, can we select an option strategy, which may be well matched to prospective market conditions? One may hedge a long currency exposure by selling futures, buying puts or selling calls. Which strategy is best and under what type of circumstances? Baseline Futures Hedge – In order to provide a comparison of various hedging strategies, let us quickly review the efficacy of a hedging strategy using short futures positions. Assume that our hedger expected the receipt of €50,000,000 which, at a hypothetical spot USD/EUR exchange rate of 1.4704, translates into a value of $73,520,000. Our hedger was concerned about protecting the value of those monies denominated in U.S.
dollars. Thus, we recommended a strategy of selling 400 CME December 2008 EuroFX futures at the prevailing futures price of 1.4605 to cover that risk. Assume that our hedger holds this position until December 5, 2008 at which point we might assume that the basis becomes fully or near fully converged, i.e., spot and futures prices are equal. What would happen under these circumstances if the spot exchange rate were (hypothetically) to decline to 1.3200; remain essentially unchanged at 1.4700; or, advance to 1.6200? If the spot exchange rate declines to 1.3200, the value of the €50,000,000 falls to $66,000,000 which implies a loss of $7,520,000 (=$73,520,000 less $66,000,000). But having sold 400 futures at 1.4605, which converge to 1.3200, that implies an offsetting profit of $7,025,000 for a net loss of $495,000. Spot USD/EUR €50MM in USD Dec ‘08 Futures Basis 8/18/08 1.4704 $73,520,000 Sell 400 @ 1.4605 -0.0099 12/05/08 1.3200 $66,000,000 Buy 400 @ 1.3200 0.0000 ($7,520,000) +$7,025,000 +0.0099 Net Loss of $495,000 In fact, if we assume full basis convergence under all circumstances regardless of the final value of the spot market, we might simulate a net loss of $495,000 consistently whether the market declines to 1.3200, remains essentially unchanged at 1.4700 or advances to 1.6200. A futures hedge allows one to “lock-in” a specific return, subject to basis risk, whether the market is bullish, bearish or neutral. 14 .
cmegroup.com/fx Spot @ 1.3200 Spot @ 1.4700 Spot @ 1.6200 Unhedged ($7,520,000) ($20,000) $7,480,000 Short Futures Hedge ($495,000) ($495,000) ($495,000) In other words, the sale of futures allows our hedger to “lock-in” a specific return, subject to some basis risk, regardless of prevailing market trends. He is protected in an adverse market, although he forfeits the potential benefits of possibly favorable exchange rate movements. How does the use of options for hedging purposes stack up against this “baseline” futures hedge? usd/eur hedged with short futures $8,000,000 Unhedged Short Futures Hedge $6,000,000 Proï¬t/Loss $4,000,000 $2,000,000 $0 -$2,000,000 -$4,000,000 -$6,000,000 1.3200 1.3350 1.3500 1.3650 1.3800 1.3950 1.4100 1.4250 1.4400 1.4550 1.4700 1.4850 1.5000 1.5150 1.5300 1.5450 1.5600 1.5750 1.5900 1.6050 1.6200 -$8,000,000 Spot USD/Euro Rate 15 Buying Protection with Puts – The idea behind the purchase of puts is to compensate loss associated with the potentially declining value of a currency with the rising intrinsic value of the puts. As the market declines, puts will go deeper and deeper in-the-money, permitting the put holder to exercise the options for a profit.
Of course, if the market should rally instead, the puts go out-of-the-money. However, having paid the option premium, the put holder’s loss is limited thereto and, of course, the favorable underlying price movement should work to the benefit of the hedger. Revisiting the previous scenario, our company wishes to hedge the anticipated future receipt of €50,000,000 (or the equivalent of $73,520,000 at a spot exchange rate of 1.4704). Assume that the company purchases 400 at-the-money December 2008 puts with a strike price of 1.4600 (with futures at 1.4605) for 0.0326.
This represents an initial net debit of $1,630,000 (= 400 x 125,000 x $0.0326). Note that we are using the same hedge ratio that was applied to the sale of futures in our short futures hedge described above. Subsequently, assume that the spot exchange rate declines from 1.4704 to 1.3200, resulting in a loss of value of $7,520,000. Held until December 5, 2008, the put options are about to expire in-themoney and are valued at their intrinsic worth of 0.1400 (= futures price of 1.3200 relative to strike price of 1.4600).
Thus, they might be exercised by selling futures at 1.4600 when they are actually valued at 1.3200, resulting in a net profit of $5,370,000 [= 400 x 125,000 x ($0.1400 - $0.0326)]. This, partially but not completely, offsets the loss of $7,520,000 in the unhedged cash value of the €50,000,000 receipt. Buying put options is akin to buying an insurance 15 policy. Long puts provide protection in a bear market. .
Managing Currency Risks with Futures Options Spot USD/EUR €50MM in USD Dec ‘08 Puts 8/18/08 1.4704 $73,520,000 Buy 400 1.4600 Puts @ 0.0326 12/05/08 1.3200 $66,000,000 Exercise 400 1.4600 Puts @ 0.1400 ($7,520,000) +$5,370,000 Net Loss of $2,150,000 Of course, if the spot market were to have remained essentially stable at 1.4700, then our hedger would have been left with slightly out-of-the-money and, therefore, worthless options by early December when expiration approached. Or, if the spot exchange rate had advanced, the hedger would likewise have essentially forfeited the initial $1,630,000 debit from the purchase of the 400 puts, but would have benefited from the market advance. A long put hedge allows you to lock-in a floor return while still retaining some upside potential. But if the market is neutral, one essentially forfeits the put premium paid up front. Spot @ 1.3200 Spot @ 1.4700 Spot @ 1.6200 Unhedged ($7,520,000) ($20,000) $7,480,000 Short Futures Hedge ($495,000) ($495,000) ($495,000) Long Put Hedge ($2,150,000) ($1,650,000) $5,850,000 As such, the long put hedge allows one to lock-in a floor return while still retaining a great deal of the upside potential associated with a possibly favorable market swing, limited to the extent that you pay the premium associated with the purchase of the put options up front. Option premiums are, of course, impacted by a variety of factors including the movement of price, time and volatility. So while the purchase of put options in the context of a hedging application reduces price risks, it also entails the acceptance of other types of risk uniquely applicable to options. Still, price impact is the foremost of these factors. 16 .
cmegroup.com/fx The degree to which you immediately reduce price risk may be found by reference to the put delta. In our example above, we utilized the purchase of at- or near-the-money put options with a delta of 0.4831 (or approximately 0.5). As such, we effectively reduce the immediate or near-term price risk by a factor of about one-half (using the appropriate futures hedge ratio). usd/eur hedged with long puts $8,000,000 Unhedged Hedged w/ 1.4600 Puts $6,000,000 The put delta may be referenced as an indication of the degree to which one offsets immediate or near-term price risk. But delta is a dynamic concept. If the market falls and the option goes in-the-money, the delta will get closer to 1.0.
If the market rises and the option goes out-of-the-money, the delta gets closer to zero. An in-the-money put with a delta of 0.60 suggests an effective 60% reduction in price risk while the use of an out-of-the-money option with a delta of 0.40 suggests a 40% reduction in price risk. Proï¬t/Loss $4,000,000 $2,000,000 $0 -$2,000,000 -$4,000,000 -$6,000,000 1.3200 1.3350 1.3500 1.3650 1.3800 1.3950 1.4100 1.4250 1.4400 1.4550 1.4700 1.4850 1.5000 1.5150 1.5300 1.5450 1.5600 1.5750 1.5900 1.6050 1.6200 -$8,000,000 Spot USD/Euro Rate 17 Delta is dynamic and gets higher as the market declines and long puts go in-the-money. Thus, long puts provide more protection when you need it. Delta gets lower as market prices advance. Thus, long puts provide less protection when you need less protection. .
Managing Currency Risks with Futures Options The dynamic nature of delta represents convexity. Convexity benefits the holder of a put insofar as it promises more protection in a bear market when you need more protection; and, less protection in a bull market when you would prefer less protection. Unfortunately, you pay for convexity by accepting negative time value decay. As expiration approaches, a near-to-the-money option will exhibit more and more time value decay or “accelerating” time value decay, or erosion.
It is interesting that the same options which experience high and rising convexity (near-term, near-the-moneys) also experience high and rising thetas. Barring a mispricing, it is impossible to experience both a positive gamma and theta when trading options. Yield Enhancement with Calls – If you believe that the market is basically stable, you might pursue a “yield enhancement” or “income augmentation” strategy by selling call options against a long cash or spot position. This is also known as “covered call writing,” in the sense that your obligation to deliver the underlying currency or futures contract, as a result of writing a call, is “covered” by the fact that you already own the currency or futures contract. The sale of calls against a long cash or spot exposure is often referred to as “covered call writing.” This strategy allows you to take advantage of an essentially neutral forecast. Thus, you must ask yourself … is the market basically volatile and, therefore, should you take advantage of convexity by buying options? Or, is the market essentially stable, recommending a strategy of taking advantage of time value decay by selling options? The purchase of puts as a hedging strategy implies that you believe that the market is volatile and want to take advantage of convexity. Revisiting the previous example, our company anticipates the receipt of €50,000,000 ($73,520,000 at a spot exchange rate of 1.4704).
Assume that the company sells 400 at-the-money December 2008 calls with a strike price of 1.4600 (with futures at 1.4605) for 0.0331. This represents an initial net credit or receipt of cash of $1,655,000 (= 400 x 125,000 x $0.0331). Again, we employ the same hedge ratio that was applied to the short futures or long put hedges. Assume that spot exchange rates fall from 1.4704 to 1.3200 for a loss of $7,520,000.
Held until December 5, 2008, the 1.4600 calls options are out-of the-money, valued at zero and therefore abandoned. Thus, our hedger retains the $1,655,000 to at least partially offset the loss of $7,520,000 … or a net loss of $5,865,000. Spot USD/EUR €50MM in USD Dec ‘08 Calls 8/18/08 1.4704 $73,520,000 Sell 400 1.4600 Calls @ 0.0331 12/05/08 1.3200 $66,000,000 Abandon 400 1.4600 Calls @ 0.0000 ($7,520,000) +$1,655,000 Net Loss of $5,865,000 18 . cmegroup.com/fx Spot @ 1.3200 Spot @ 1.4700 Spot @ 1.6200 Unhedged ($7,520,000) ($20,000) $7,480,000 Short Futures Hedge ($495,000) ($495,000) ($495,000) Long Put Hedge ($2,150,000) ($1,650,000) $5,850,000 Short Call Hedge ($5,865,000) $1,135,000 $1,135,000 Had the spot market remained stable at 1.4700, then our hedger would have had slightly in-the-money options which would be exercised against him such that he would have retained most of the initial net credit. Or, if the spot exchange rate had advanced sharply to 1.6200, the benefits of the favorable exchange rate movement would essentially be offset by a loss in the value of the short calls, although the hedger would still benefit to the extent of the initial net credit of $1,655,00. The short call strategy implies that you lock-in a ceiling return, limiting your ability to participate in any upside potential. The covered call writer is compensated, however, to the extent that he receives the option premium, which at least partially offsets downside losses. While a long put hedge enables you to take advantage of convexity albeit while suffering the ill effects of time value decay.
The short call hedge is just the opposite insofar as it allows you to capitalize on time value decay while suffering from the potentially ill effects of convexity. The sale of call options against a lock spot exposure allows you to lock-in a ceiling return, limiting your ability to participate in possibly favorable market movements. But if the market should remain stable, one may enhance returns by retaining the premium whose time value will decay as expiration approaches. 19 . Managing Currency Risks with Futures Options usd/eur hedged with short calls $8,000,000 Unhedged Hedged w/ 1.4600 Calls $6,000,000 In- and Out-of-the-Money Options – Thus far, we have focused on the use of at- or at least near-to-the-money options in the context of our hedging strategies. But let us consider the use of in- and out-of-themoney long puts or short calls as an alternative. $4,000,000 Proï¬t/Loss The short call hedge works best when the market remains basically stable. In this case, time value decay results in a gradual decline in the premium. Thus, you “capture” the premium, enhancing yield. $2,000,000 $0 -$2,000,000 -$4,000,000 -$6,000,000 1.3200 1.3350 1.3500 1.3650 1.3800 1.3950 1.4100 1.4250 1.4400 1.4550 1.4700 1.4850 1.5000 1.5150 1.5300 1.5450 1.5600 1.5750 1.5900 1.6050 1.6200 -$8,000,000 Spot USD/Euro Rate Convexity and volatility are closely related concepts.
It is only when the market is volatile, when it is moving either up or down, that the effects of convexity are actually observed. If the market is moving and volatility is rising, the short calls may rise in value, resulting in loss. If the market should advance, the calls will go in-the-money, the delta approaching 1.0. The growing intrinsic value of the calls presumably offsets profit in the rising value of the cash security resulting in an offset.
Fortunately, this return is positive by virtue of the initial receipt of the option premium. If the market should decline, the calls go out-of-the-money, eventually expiring worthless as the delta approaches zero. Still, the hedger is better off having hedged by virtue of the receipt of the premium up front. As a general rule, you tend to “get what you pay for.” The purchase of the expensive in-the-money puts entails a much larger up-front investment, but you buy more protection in the event of a market downturn.
For example, rather than buying the 1.4600 at-themoney puts for a premium of 0.0326, our hedger might have purchased in-the-money puts struck at 1.4900 for a premium of 0.0496. By contrast, the purchase of the cheap out-of-the-moneys entails a much smaller up-front debit to your account. For example, our hedger might have purchased out-of-the-money puts with an exercise price of 1.4300 for a premium of 0.0203.
But, you get less protection in a downturn. One may use in-, at- or out-of-the-money options as part of a hedging strategy. As a general rule, you get what you pay for. Expensive in-themoney options tend to provide more protection at the risk of limiting your ability to participate in potentially favorable market movements. A short call hedge works best in a stable market environment. 20 .
cmegroup.com/fx usd/eur hedged with Long puts $8,000,000 Unhedged Hedged w/ 1.4300 Puts Hedged w/ 1.4600 Puts Hedged w/ 1.4900 Puts $6,000,000 Proï¬t/Loss $4,000,000 $2,000,000 $0 -$2,000,000 -$4,000,000 -$6,000,000 1.3200 1.3350 1.3500 1.3650 1.3800 1.3950 1.4100 1.4250 1.4400 1.4550 1.4700 1.4850 1.5000 1.5150 1.5300 1.5450 1.5600 1.5750 1.5900 1.6050 1.6200 -$8,000,000 Spot USD/Euro Rate The purchase of a put allows you to “lock-in” a floor or minimum return. But that floor is only realized at prices at or below the strike price. The high-struck in-the-moneys provide protection at all levels from 1.4900 and down. The low-struck out-of-the-moneys provide protection only from levels of 1.4300 and below. Expensive in-the-money puts provide more protection.
Cheap out-of-the-money puts provide less protection. By contrast, the cheap in-the-money puts allow you to retain greater ability to participate in possible upward price advances than do the expensive out-of-the-moneys. Remember that at all prices at or above the strike price, one’s returns are restrained by the initial forfeiture of the option premium. The purchase of the expensive inthe-money puts places a greater burden on one’s portfolio than do the cheap out-of-the-moneys. The same general principles may be said to apply to the sale of expensive in-the-money calls vs.
the sale of cheap out-of-the-money calls. For example, rather than selling at-the-money 1.4600 calls for a premium of 0.0331, one might have sold in-the-money calls struck at 1.4300 for a premium of 0.0506; or, out-of-the-money calls struck at 1.4900 for a premium of 0.0203. Likewise, the sale of expensive in-the-money calls provides more protection while the sale of cheap out-of-the-money calls provides more protection. One receives protection from downside risk by selling calls through the initial receipt of the option premium. Thus, the higher that premium, the greater the degree of protection.
If the market should advance above the option strike price, however, the short calls go inthe-money and generate a loss at a loss, which offsets the increase in the value of the cash securities. Thus, the sale of in-the-money 1.4300 calls provides the greatest degree of protection in the event of a market decline. On the other extreme, the sale of out-of-the-money 1.4900 calls provides the thinnest margin of protection. But if the market should advance, the sale of the cheap out-of-the-money calls allows one to participate to a much greater degree in the rally.
The sale of expensive in-themoney calls offers the least amount of upside participation. 21 . Managing Currency Risks with Futures Options usd/eur hedged with short Calls $8,000,000 Unhedged Hedged w/ 1.4300 Calls Hedged w/ 1.4600 Calls Hedged w/ 1.4900 Calls $6,000,000 Proï¬t/Loss $4,000,000 $2,000,000 Matching Strategy with Forecast – Note that by buying puts against a long cash portfolio, the risk/reward profile associated with the entire position strongly resembles that of an outright long call. As such, this strategy is sometimes referred to as a “synthetic long call.” Likewise, the combination of selling calls against a long securities portfolio will strongly resemble the outright sale of a put. Thus, we sometimes refer to this strategy as a “synthetic short put.” $0 A prudent hedger may try to match his price forecast with the most beneficial hedging strategy. -$2,000,000 -$4,000,000 -$6,000,000 1.3200 1.3350 1.3500 1.3650 1.3800 1.3950 1.4100 1.4250 1.4400 1.4550 1.4700 1.4850 1.5000 1.5150 1.5300 1.5450 1.5600 1.5750 1.5900 1.6050 1.6200 -$8,000,000 Spot USD/Euro Rate Note, however, that the sale of calls options against a long spot position generally is considered a neutral strategy. One sells options to capitalize on time value decay in a stagnant market environment. Clearly, the sale of the at-the-moneys generates the most attractive return when yields remain stable.
This makes sense as the atthe-moneys have the greatest amount of time value to begin and experience the greatest degree of time value decay, as evidenced by their generally high thetas. Many textbooks draw a strong distinction between hedging or riskmanagement and speculative activity. We are not so sure that this distinction is warranted. Obviously, the same factors that might motivate a speculator to buy calls might motivate a hedger to buy puts against his cash portfolio.
And, the same factors that might motivate a speculator to sell puts might motivate a hedger to sell calls against his cash portfolio. How might we define hedging vs. speculative activity? Clearly a speculator is someone who might use futures and options in an attempt to make money. A hedger is someone who might use futures and options selectively in an attempt to make money and who already holds a cash position.
Perhaps this distinction is a bit cynical. It is, however, thoroughly practical. It is sometimes difficult to distinguish between speculation and “selective” hedging. 22 . cmegroup.com/fx The conclusion which might be reached from this discussion is that the necessity of making a price forecast is just as relevant from the hedger’s viewpoint as it is from the speculator’s viewpoint. Which one of our three basic hedge strategies: sell futures, buy puts or sell calls, is best? Clearly, that depends upon the market circumstances. In a bearish environment, where the holder of a cash portfolio needs to hedge the most, the alternative of selling futures is clearly superior to that of buying puts or selling calls. In a neutral environment, the sale of calls is superior, followed by the sale of futures and the purchase of puts. The best alternative in a bull market is simply not to hedge.
However, if one must attempt to limit risk, the best hedge alternative is to purchase of puts, followed by the sale of calls and the sale of futures. Matching Hedging Strategy with Forecast Bearish Neutral Bullish 1 Sell Futures Sell Calls Buy Puts 2 Buy Puts Sell Futures Sell Calls 3 Sell Calls Buy Puts Sell Futures Note that no single strategy is systematically or inherently superior to any other. Each achieves a number 1, 2 and 3 ranking, underscoring the speculative element in hedging. 23 A short futures hedge works best in a very bearish market environment. A long put hedge provides a good measure of downside protection but preserves one’s ability to benefit from a possibly favorable market advance.
Finally, a short call hedge is recommended in a neutral market environment. Collar Strategy – The concept of a long put hedge is very appealing to the extent that it provides limited downside risk while retaining at least a partial ability to participate in potential upside price movement. The problem with buying put options is, of course, the necessity to actually pay for the premium. Thus, some strategists have looked to strategies, which might at least partially offset the cost associated with the purchase of put options. One might, for example, combine the purchase of put options with the sale of call options.
If one were to buy puts and sell calls at the same strike price, the resulting risks and returns would strongly resemble that of a short futures position. As a result, the combination of long puts and short calls at the same strike price is often referred to as a “synthetic short futures position.” Barring a market mispricing, however, there is no apparent advantage to assuming a synthetic as opposed to an actual futures position as part of a hedging strategy. . Managing Currency Risks with Futures Options A collar is constructed through the sale of high-struck call options and the purchase of lower-struck put options. usd/eur hedged with Collar Unhedged $3,000,000 Hedged $2,000,000 For example, assume that you sell 400 of the 1.4600 at-the-money calls at 0.0331 for a credit of $1,655,000 and simultaneously buy 400 of the 1.4300 out-of-the-money puts at 0.0203 for a debit of $1,015,000. This results in a net credit or inflow of cash equivalent to $640,000. This strategy combines some of the benefits of both buying puts and selling calls. The net result of a collar is that you establish both a floor and a ceiling return. $0 -$1,000,000 -$2,000,000 -$3,000,000 -$4,000,000 1.5150 1.5075 1.4925 1.5000 1.4775 1.4850 1.4625 1.4700 1.4475 1.4550 1.4325 1.4400 1.4175 1.4250 1.4100 1.4025 1.3875 1.3950 -$5,000,000 1.3800 But if one were to sell near-to-the money calls and purchase lower struck and somewhat out-of-the-money puts, one could create an altogether different type of risk exposure. This position might allow you to capture some premium in a neutral market as a result of the accelerated time value decay associated with the short calls while enjoying the floor return associated with the long put hedge in the event of a market decline.
On the downside, this strategy limits one’s ability to participate in potential market advances. In other words, this strategy entails the elements of both a long put hedge and a short call hedge … i.e., you lock in both a floor and a ceiling return. Proï¬t/Loss $1,000,000 Spot USD/Euro Rate A collar is most highly recommended when one has a generally neutral to negative market outlook. There are many variations on this theme including the possibility of buying higher struck puts and selling lower struck calls or a “reverse collar.” This strategy might enhance one’s returns in a bear market but comes at the risk of reducing one’s ability to participate in a possibly upside market move even more severely. A collar may be recommended in a neutral to negative market environment. 24 .
cmegroup.com/fx Delta Neutral Hedge – Options are extremely versatile instruments and there are many variations on the risk-management theme. In particular, it is always enticing to attempt to find a way to take advantage of the beneficial effects associated with options while minimizing the unfortunate effects that come as part of the package through a system of active management. Many of these systems rely upon the concept of delta as a central measure of risk and are known as “delta neutral” strategies. As an illustration, consider our hedger with the prospective receipt of €50,000,000 intent on hedging the risk of a falling euro vs. the U.S. dollar.
One might buy put options or sell call options against a long exposure with the intention of matching the net deltas. He may elect to sell 400 call options on EuroFX futures by reference to the futures hedge ratio. Or, the hedge may be weighted by reference to delta.
The appropriate “delta neutral hedge ratio” is readily determined by taking the reciprocal of the delta. A delta neutral hedging strategy calls for active management of an option position in such as way as to maintain a net delta near zero. 25 Delta Neutral Hedge Ratio = Futures Hedge Ratio ÷ Option Delta In our previous examples, we had considered the sale of 400 at-themoney 1.4600 call options with a delta of 0.5104. Employing a delta weighted strategy, the hedger might elect to utilize 828 options instead. Delta Neutral Hedge Ratio = Futures Hedge Ratio ÷ Option Delta = 400 ÷ 0.5104 = 784 options A delta neutral hedge ratio may be calculated by reference to the reciprocal of the option delta. But because delta is a dynamic concept, this strategy implies some rather active management. For example, as the market rallies and the calls go into-the-money, the call delta will start to increase, resulting in accelerating losses if no action is taken.
Thus, our hedger should reduce the size of the short call position as the market advances. For example, if the option delta advances from 0.5104 to 0.5500, this implies that the hedge ratio will decline to 727 positions (= 400 ÷ 0.5500). Thus, one might buy-back or liquidate some 57 positions as the market advances. .
Managing Currency Risks with Futures Options If you sell calls in a delta neutral manner, you may find it necessary to sell more calls as the market declines and liquidate calls as the market advances. If the market declines, the calls will go out-of-the-money and the call delta will fall. This too will result in accelerating net losses to the extent that the options will provide increasingly less protection as the market breaks. Thus, our hedger might sell more options on the way down. For example, if the call delta declines to 0.4800, this implies that the hedge ratio will advance to 833 positions (= 400 ÷ 0.4800). Thus, one might sell an additional 49 calls as the market declines. The application of a delta hedge strategy with the use of short calls implies an essentially neutral market forecast.
This is intuitive to the extent that the sale of call options implies that one wishes to take advantage of time value decay in an essentially sideways trending market environment. But sometimes the market does not cooperate. In particular, this strategy entails the risk of whipsaw markets, i.e., the possibility that one buys back positions on the way up and sells more on the way down. Thus, whipsaws may have you buying high and selling low as the market reverses from one direction to the other.
The perils of a whipsaw market imply that one might couple this strategy with a diligent effort in creating market forecasting tools specifically to avoid the ill effects of whipsaws. Instead of the use of call options as part of a delta neutral strategy, one might also consider the purchase of put options. A delta neutral hedging strategy entails the risk of whipsaw markets, i.e., the possibility that one is caught buying high and selling lows as part of the adjustment of the strategy. One might buy the at-the-money 1.4600 put options with a delta of 0.4831. Our formula suggests that one might utilize 828 options to neutralize one’s risk exposure as measured by delta. Delta Neutral Hedge Ratio = Futures Hedge Ratio ÷ Option Delta = 400 ÷ 0.4831 = 828 options 26 .
cmegroup.com/fx As was the case with our delta neutral short call hedge, we know that the put delta will be sensitive to changing market conditions. If, for example, the market were to decline, the puts will go intothe-money and the delta will increase. This implies that one might liquidate some of the long puts to maintain a delta neutral stance. Or, if the market advances, this implies that the put options may go out-of-the-money and the delta will decrease. This may suggest that you purchase more puts to maintain a delta neutral stance. However, one might observe that as the market declines, the put options essentially provide more protection just when you need it most by virtue of the advancing delta. Or, that the put options will provide less protection as the market advances by virtue of a declining delta at a point.
This calls the question … why adjust the hedge ratio when the options are “self-adjusting” in a beneficial way? Of course, the risk of this strategy is that the market might simply remain stagnant and the hedger is subject to the ill effects of time value decay. As such, the use of long options is a hedging strategy most aptly recommended in a volatile market environment. One may pursue a delta neutral strategy with the use of long put options. However, long puts are essentially self-adjusting in the sense that they provide more protection as the market moves adversely and less protection when the market moves favorably.
Thus, it is not clear whether one really needs to adjust the hedge ratio at all in this context. For more information on CME Group FX, visit www.cmegroup.com/fx. CME GROUP HEADQUARTERS 20 South Wacker Drive Chicago, Illinois 60606 cmegroup.com CME GROUP REGIONAL OFFICES info@cmegroup.com 800 331 3332 312 930 1000 New York 212 299 2000 London + 44 20 7796 7100 São Paulo Houston 713 658 9292 Washington D.C. 202 638 3838 +55 11 2565 5999 Singapore +65 6593 5555 Tokyo +81 3 5403 4828 Futures trading is not suitable for all investors, and involves the risk of loss. Futures are a leveraged investment, and because only a percentage of a contract’s value is required to trade, it is possible to lose more than the amount of money deposited for a futures position. Therefore, traders should only use funds that they can afford to lose without affecting their lifestyles.
And only a portion of those funds should be devoted to any one trade because they cannot expect to profit on every trade. All references to options refer to options on futures. CME Group is a trademark of CME Group Inc. The Globe Logo, CME, and Chicago Mercantile Exchange are trademarks of Chicago Mercantile Exchange Inc.
CBOT and the Chicago Board of Trade are trademarks of the Board of Trade of the City of Chicago, Inc. NYMEX is a registered trademark of the New York Mercantile Exchange, Inc. All other trademarks are the property of their respective owners. The information within this brochure has been compiled by CME Group for general purposes only.
CME Group assumes no responsibility for any errors or omissions. Additionally, all examples in this brochure are hypothetical situations, used for explanation purposes only, and should not be considered investment advice or the results of actual market experience. All matters pertaining to rules and specifications herein are made subject to and are superseded by official CME, CBOT and NYMEX rules.
Current rules should be consulted in all cases concerning contract specifications. Copyright © 2010 CME Group. All rights reserved. FX262/0/0410 .